题目内容
已知函数 .
.
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
 .
.(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m≤2时,证明f(x)>0.
(1)m=1(讨论见解析);
(2)见解析.
(2)见解析.
(1)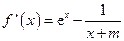 .
.
由x=0是f(x)的极值点得f '(0)=0,所以m=1.
于是f(x)=ex-ln(x+1),定义域为(-1,+∞),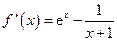 .
.
函数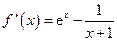 在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.
在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.
所以f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增.
(2)当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时, f(x)>0.
当m=2时,函数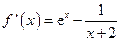 在(-2,+∞)上单调递增.
在(-2,+∞)上单调递增.
又f '(-1)<0, f '(0)>0,故f '(x)=0在(-2,+∞)上有唯一实根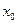 ,且
,且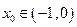 .
.
当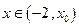 时, f '(x)<0;当
时, f '(x)<0;当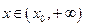 时, f '(x)>0,从而当
时, f '(x)>0,从而当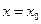 时,f(x)取得最小值.
时,f(x)取得最小值.
由f '(x0)=0得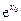 =
=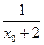 ,
,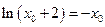 ,
,
故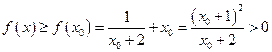 .
.
综上,当m≤2时, f(x)>0.
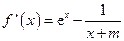 .
.由x=0是f(x)的极值点得f '(0)=0,所以m=1.
于是f(x)=ex-ln(x+1),定义域为(-1,+∞),
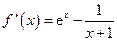 .
.函数
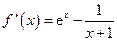 在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.
在(-1,+∞)上单调递增,且f '(0)=0,因此当x∈(-1,0)时, f '(x)<0;当x∈(0,+∞)时, f '(x)>0.所以f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增.
(2)当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时, f(x)>0.
当m=2时,函数
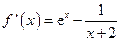 在(-2,+∞)上单调递增.
在(-2,+∞)上单调递增.又f '(-1)<0, f '(0)>0,故f '(x)=0在(-2,+∞)上有唯一实根
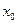 ,且
,且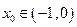 .
.当
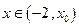 时, f '(x)<0;当
时, f '(x)<0;当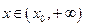 时, f '(x)>0,从而当
时, f '(x)>0,从而当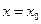 时,f(x)取得最小值.
时,f(x)取得最小值.由f '(x0)=0得
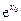 =
=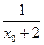 ,
,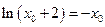 ,
,故
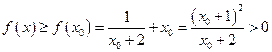 .
.综上,当m≤2时, f(x)>0.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 R).
R). 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值; 的单调区间和极值;
的单调区间和极值; ,且
,且 时,证明:
时,证明:
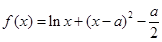 ,
,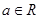 .
. 在
在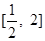 上单调递增,求实数
上单调递增,求实数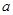 的取值范围;
的取值范围;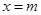 为函数
为函数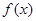 的图象与
的图象与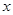 轴交于
轴交于 两点,且
两点,且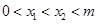 ,
,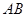 中点为
中点为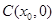 ,
,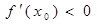 .
.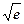 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。 是可导的函数,且
是可导的函数,且 对于
对于 恒成立,则( )
恒成立,则( )
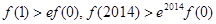


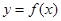 的导函数的图像,现有四种说法:
的导函数的图像,现有四种说法:
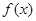 在
在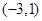 上是增函数;
上是增函数;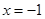 是
是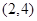 上是减函数,在
上是减函数,在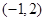 上是增函数;
上是增函数;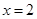 是
是 的单调递增区间是_____________.
的单调递增区间是_____________. 的导函数为
的导函数为 ,若
,若 ,则
,则 .
.