题目内容
已知函数f(x)=(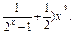
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性;
(3)证明:f(x)>0.
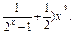
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性;
(3)证明:f(x)>0.
(1)定义域为(-∞,0)∪(0,+∞)(2)f(x)=(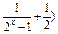 x3是偶函数(3)证明见解析
x3是偶函数(3)证明见解析
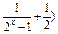 x3是偶函数(3)证明见解析
x3是偶函数(3)证明见解析(1)解 由2x-1≠0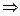 x≠0,∴定义域为(-∞,0)∪(0,+∞).
x≠0,∴定义域为(-∞,0)∪(0,+∞).
(2)解 f(x)=(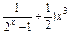
可化为f(x)=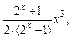
则f(-x)=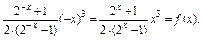
∴f(x)=(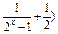 x3是偶函数.
x3是偶函数.
(3)证明 当x>0时,2x>1,x3>0.
∴(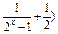 x3>0.
x3>0.
∵f(x)为偶函数,∴当x<0时,f(x)=f(-x)>0.
综上可得f(x)>0.
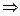 x≠0,∴定义域为(-∞,0)∪(0,+∞).
x≠0,∴定义域为(-∞,0)∪(0,+∞).(2)解 f(x)=(
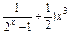
可化为f(x)=
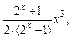
则f(-x)=
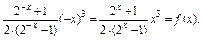
∴f(x)=(
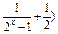 x3是偶函数.
x3是偶函数.(3)证明 当x>0时,2x>1,x3>0.
∴(
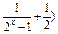 x3>0.
x3>0.∵f(x)为偶函数,∴当x<0时,f(x)=f(-x)>0.
综上可得f(x)>0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
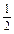 x,求使f(x)=-
x,求使f(x)=-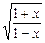 ;
;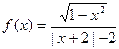 ;(4)
;(4)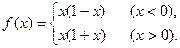
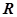 上的函数
上的函数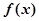 是奇函数且满足
是奇函数且满足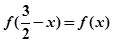 ,
,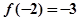 ,则
,则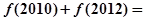 ( )
( )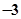
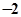
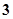
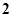
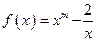 且
且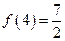 ,
,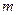 的值;
的值;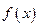 的奇偶性;
的奇偶性;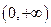 上的单调性,并给予证明.
上的单调性,并给予证明.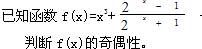
 内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围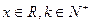 ,定义
,定义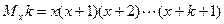 ,例
,例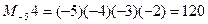 ,则函数
,则函数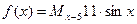 是( )
是( )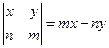 .设函数
.设函数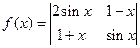 ,则函数
,则函数 是
是