题目内容
判断下列函数的奇偶性:
(1)f(x)=|x+1|-|x-1|;(2)f(x)=(x-1)·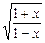 ;
;
(3)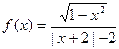 ;(4)
;(4)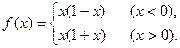
(1)f(x)=|x+1|-|x-1|;(2)f(x)=(x-1)·
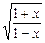 ;
;(3)
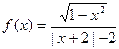 ;(4)
;(4)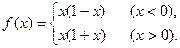
⑴奇函数,⑵既不是奇函数也不是偶函数,⑶奇函数,⑷奇函数
判断函数的奇偶性应依照定义解决,但都要先考查函数的定义域。
(1)函数的定义域x∈(-∞,+∞),对称于原点.
∵f(-x)=|-x+1|-|-x-1|=|x-1|-|x+1|=-(|x+1|-|x-1|)=-f(x),
∴f(x)=|x+1|-|x-1|是奇函数.
(2)先确定函数的定义域.由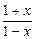 ≥0,得-1≤x<1,其定义域不对称于原点,所以f(x)既不是奇函数也不是偶函数.
≥0,得-1≤x<1,其定义域不对称于原点,所以f(x)既不是奇函数也不是偶函数.
(3)去掉绝对值符号,根据定义判断.
由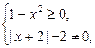 得
得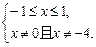
故f(x)的定义域为[-1,0)∪(0,1],关于原点对称,且有x+2>0.
从而有f(x)=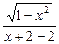 =
=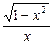 ,∴f(-x)=
,∴f(-x)=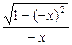 =-
=-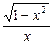 =-f(x)
=-f(x)
故f(x)为奇函数.
(4)∵函数f(x)的定义域是(-∞,0)∪(0,+∞),并且当x>0时,-x<0,
∴f(-x)=(-x)[1-(-x)]=-x(1+x)=-f(x)(x>0).
当x<0时,-x>0,∴f(-x)=-x(1-x)=-f(x)(x<0).
故函数f(x)为奇函数.
1函数的奇偶性是函数的一个整体性质, 定义域具有对称性 ( 即若奇函数或偶函数的定义域为D, 则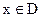 时
时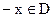 ) 是一个函数为奇函数或偶函数的必要条件
) 是一个函数为奇函数或偶函数的必要条件
2分段函数的奇偶性一般要分段证明.③判断函数的奇偶性应先求定义域再化简函数解析式.
题型2:证明抽象函数的奇偶性
(1)函数的定义域x∈(-∞,+∞),对称于原点.
∵f(-x)=|-x+1|-|-x-1|=|x-1|-|x+1|=-(|x+1|-|x-1|)=-f(x),
∴f(x)=|x+1|-|x-1|是奇函数.
(2)先确定函数的定义域.由
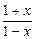 ≥0,得-1≤x<1,其定义域不对称于原点,所以f(x)既不是奇函数也不是偶函数.
≥0,得-1≤x<1,其定义域不对称于原点,所以f(x)既不是奇函数也不是偶函数.(3)去掉绝对值符号,根据定义判断.
由
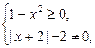 得
得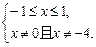
故f(x)的定义域为[-1,0)∪(0,1],关于原点对称,且有x+2>0.
从而有f(x)=
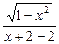 =
=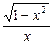 ,∴f(-x)=
,∴f(-x)=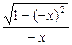 =-
=-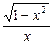 =-f(x)
=-f(x)故f(x)为奇函数.
(4)∵函数f(x)的定义域是(-∞,0)∪(0,+∞),并且当x>0时,-x<0,
∴f(-x)=(-x)[1-(-x)]=-x(1+x)=-f(x)(x>0).
当x<0时,-x>0,∴f(-x)=-x(1-x)=-f(x)(x<0).
故函数f(x)为奇函数.
1函数的奇偶性是函数的一个整体性质, 定义域具有对称性 ( 即若奇函数或偶函数的定义域为D, 则
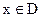 时
时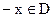 ) 是一个函数为奇函数或偶函数的必要条件
) 是一个函数为奇函数或偶函数的必要条件2分段函数的奇偶性一般要分段证明.③判断函数的奇偶性应先求定义域再化简函数解析式.
题型2:证明抽象函数的奇偶性

练习册系列答案
相关题目
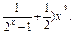
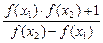 ;
; 求证:
求证: 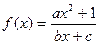 (a、b、c∈Z)是奇函数,又
(a、b、c∈Z)是奇函数,又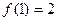 ,
,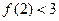 ,求a、b、c的值.
,求a、b、c的值.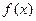 是定义在
是定义在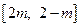 上的奇函数,且对任意
上的奇函数,且对任意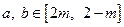 ,当
,当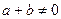 时,都有
时,都有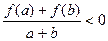 .(Ⅰ)求实数
.(Ⅰ)求实数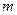 的值;(Ⅱ)解不等式
的值;(Ⅱ)解不等式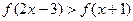 .
.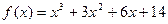 ,且
,且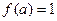 ,
,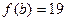 ,则
,则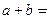 ( )
( )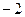
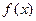 =
=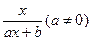 的图像过点(-4,4),且关于直线
的图像过点(-4,4),且关于直线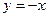 成轴对称图形,试确定
成轴对称图形,试确定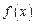 是
是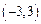 上的奇函数,当
上的奇函数,当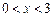 时,
时,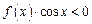 的解集是( )
的解集是( )