题目内容
10.设变量x,y满足约束条件$\left\{{\begin{array}{l}x-y≤0\\ x+y<1\\ 2x+y≥1\end{array}}\right.$,则目标函数z=-2y-3x的( )| A. | 最大值为$-\frac{5}{3}$,最小值为$-\frac{5}{2}$ | B. | 最大值为$-\frac{5}{3}$,最小值不存在 | ||
| C. | 最大值为-2,最小值不存在 | D. | 最大值不存在,最小值为$-\frac{5}{2}$ |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答 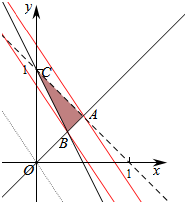 解:作出不等式组对于的平面区域如图:
解:作出不等式组对于的平面区域如图:
由z=-2y-3x,则y=$-\frac{3}{2}$x-$\frac{z}{2}$,
平移直线y=$-\frac{3}{2}$x-$\frac{z}{2}$,
由图象可知当直线y=$-\frac{3}{2}$x-$\frac{z}{2}$经过点A时,直线y=$-\frac{3}{2}$x-$\frac{z}{2}$的截距最大,此时z最小,
经过点B时,直线y=$-\frac{3}{2}$x-$\frac{z}{2}$的截距最小,此时z最大,
由$\left\{\begin{array}{l}{x-y=0}\\{x+y=1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{1}{2}}\end{array}\right.$,即A($\frac{1}{2}$,$\frac{1}{2}$)
由$\left\{\begin{array}{l}{x-y=0}\\{2x+y=1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{1}{3}}\end{array}\right.$,即B($\frac{1}{3}$,$\frac{1}{3}$)
此时zmin=-2×$\frac{1}{2}$-3×$\frac{1}{2}$=$-\frac{5}{2}$,
zmax=-2×$\frac{1}{3}$-3×$\frac{1}{3}$=$-\frac{5}{3}$,
故$-\frac{5}{2}$<z≤$-\frac{5}{3}$,
即最大值为$-\frac{5}{3}$,最小值不存在,
故选:B
点评 本题主要考查线性规划的应用,利用z的几何意义,利用数形结合是解决本题的关键.

| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | -3 |
| A. | (4,5) | B. | (-2,2) | C. | (3,5) | D. | (-2,1) |

(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
| 生产能手 | 非生产能手 | 合计 | |
| 25周岁以上组 | |||
| 25周岁以下组 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
| A. | $\frac{1}{2010}$ | B. | $\frac{1}{2011}$ | C. | $\frac{2010}{2011}$ | D. | $\frac{1}{2}$ |