题目内容
2.如果1+2i是实系数一元二次方程x2+ax+b=0的根,求a+b的值.分析 由实系数一元二次方程根的特点可得1-2i也是实系数一元二次方程x2+ax+b=0的根,由韦达定理可得.
解答 解:∵1+2i是实系数一元二次方程x2+ax+b=0的根,
∴1-2i也是实系数一元二次方程x2+ax+b=0的根,
由韦达定理可得(1+2i)+(1-2i)=-a且(1+2i)(1-2i)=b,
∴a=-2,b=1-4i2=5,∴a+b=3
点评 本题考查复数的代数形式的运算,涉及韦达定理,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若a,b∈R且a+b=0,则2a+2b的最小值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.设变量x,y满足约束条件$\left\{{\begin{array}{l}x-y≤0\\ x+y<1\\ 2x+y≥1\end{array}}\right.$,则目标函数z=-2y-3x的( )
| A. | 最大值为$-\frac{5}{3}$,最小值为$-\frac{5}{2}$ | B. | 最大值为$-\frac{5}{3}$,最小值不存在 | ||
| C. | 最大值为-2,最小值不存在 | D. | 最大值不存在,最小值为$-\frac{5}{2}$ |
11.△ABC内接于以O为圆心,1为半径的圆,且3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$,则△AOB的面积=( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | 1 | D. | $\frac{1}{2}$ |
12.记者要为四名学生和他们的一名老师拍照,要求他们排成一排,老师必须站在正中间,则不同的排法共有( )
| A. | 120种 | B. | 72种 | C. | 56种 | D. | 24种 |
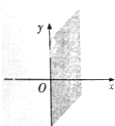 用弧度制表示终边落在阴影区域内角的集合{α|-$\frac{π}{2}$+2kπ≤α≤$\frac{π}{2}$+2kπ,k∈Z}.
用弧度制表示终边落在阴影区域内角的集合{α|-$\frac{π}{2}$+2kπ≤α≤$\frac{π}{2}$+2kπ,k∈Z}.