题目内容
5.某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.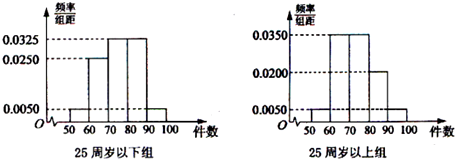
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
| 生产能手 | 非生产能手 | 合计 | |
| 25周岁以上组 | |||
| 25周岁以下组 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
分析 (1)由分层抽样的特点可得样本中有25周岁以上、下组工人人数,再由所对应的频率可得样本中日平均生产件数不足60件的工人中,25周岁以上、下组工人的人数分别为3,2,由古典概型的概率公式可得答案;
(2)由频率分布直方图可得“25周岁以上组”中的生产能手的人数,以及“25周岁以下组”中的生产能手的人数,据此可得2×2列联表,可得k2≈1.79,由1.79<2.706,可得结论.
解答 解:(1)由已知可得,样本中有25周岁以上组工人100×$\frac{300}{300+200}$=60名,
25周岁以下组工人100×$\frac{200}{300+200}$=40名,
所以样本中日平均生产件数不足60件的工人中,25周岁以上组工人有60×0.05=3(人),
25周岁以下组工人有40×0.05=2(人),
故从中随机抽取2名工人所有可能的结果共${C}_{5}^{2}$=10种,
其中至少1名“25周岁以下组”工人的结果共${C}_{3}^{1}$•${C}_{2}^{1}$+${C}_{2}^{2}$=7种,
故所求的概率为:$\frac{7}{10}$;
(2)由频率分布直方图可知:在抽取的100名工人中,“25周岁以上组”中的生产能手有60×0.25=15(人),
“25周岁以下组”中的生产能手有40×0.375=15(人),据此可得2×2列联表如下:
| 生产能手 | 非生产能手 | 合计 | |
| 25周岁以上组 | 15 | 45 | 60 |
| 25周岁以下组 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
因为1.79<2.706,所以没有90%的把握认为“生产能手与工人所在的年龄组有关”.
点评 本题考查独立性检验,涉及频率分布直方图,以及古典概型的概率公式,属中档题.

练习册系列答案
相关题目
16.方程|y|-1=$\sqrt{1-(x-1)^{2}}$表示的曲线是( )
| A. | 两个半圆 | B. | 两个圆 | C. | 抛物线 | D. | 一个圆 |
20.设i为虚数单位,若复数z=(m2+2m-8)+(m-2)i是纯虚数,则实数m=( )
| A. | 2 | B. | -4或2 | C. | 2或-4 | D. | -4 |
10.设变量x,y满足约束条件$\left\{{\begin{array}{l}x-y≤0\\ x+y<1\\ 2x+y≥1\end{array}}\right.$,则目标函数z=-2y-3x的( )
| A. | 最大值为$-\frac{5}{3}$,最小值为$-\frac{5}{2}$ | B. | 最大值为$-\frac{5}{3}$,最小值不存在 | ||
| C. | 最大值为-2,最小值不存在 | D. | 最大值不存在,最小值为$-\frac{5}{2}$ |