题目内容
18.设变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}}\right.$,且目标函数z=ax+y仅在点(2,1)处取得最小值,则实数a的取值范围是( )| A. | (4,5) | B. | (-2,2) | C. | (3,5) | D. | (-2,1) |
分析 作出不等式对应的平面区域,利用线性规划的知识,确定目标取最优解的条件,即可求出a的取值范围.
解答 解:作出不等式对应的平面区域,
由z=ax+y得y=-ax+z,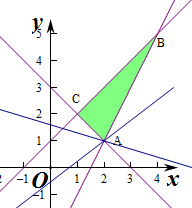
解:可行域为△ABC,如图,
由z=ax+y可得y=-ax+z,直线的斜率k=-a
∵kAB=2,kAC=-1
若目标函数z=ax+y仅在点A(2,1)处取得最小值,则有kAC<k<kAB
即-1<-a<2
∴-2<a<1
故选:D
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.根据条件目标函数z=ax+y仅在点A(2,1)处取得最小值,确定直线的位置是解决本题的关键.

练习册系列答案
相关题目
9.已知集合A={1,2,3,4},B={(x,y)|x∈A,y∈A,xy∈A},则集合B的所有真子集的个数为( )
| A. | 512 | B. | 256 | C. | 255 | D. | 254 |
10.设变量x,y满足约束条件$\left\{{\begin{array}{l}x-y≤0\\ x+y<1\\ 2x+y≥1\end{array}}\right.$,则目标函数z=-2y-3x的( )
| A. | 最大值为$-\frac{5}{3}$,最小值为$-\frac{5}{2}$ | B. | 最大值为$-\frac{5}{3}$,最小值不存在 | ||
| C. | 最大值为-2,最小值不存在 | D. | 最大值不存在,最小值为$-\frac{5}{2}$ |
8.已知正三棱锥P-ABC,点P、A、B、C都在半径为$\sqrt{3}$的球面上,若PA、PB、PC两两互相垂直,则球心到截面ABC的距离为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
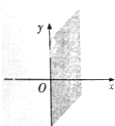 用弧度制表示终边落在阴影区域内角的集合{α|-$\frac{π}{2}$+2kπ≤α≤$\frac{π}{2}$+2kπ,k∈Z}.
用弧度制表示终边落在阴影区域内角的集合{α|-$\frac{π}{2}$+2kπ≤α≤$\frac{π}{2}$+2kπ,k∈Z}.