题目内容
15.过点A(-$\sqrt{6}$,0)和抛物线x2=2py焦点F的直线与抛物线相交于点B,且$\overrightarrow{AF}$=2$\overrightarrow{FB}$.(1)求抛物线的方程;
(2)M,N为抛物线上两点,O为原点,$\overrightarrow{OM}$•$\overrightarrow{ON}$=-1,过M,N分别作抛物线的两条切线,相交于P点,求△PMN面积的最小值.
分析 (1)利用Rt△AOF与Rt△ACB相似,计算即得结论;
(2)通过设直线MN的方程y=kx+b,并与抛物线方程联立,通过$\overrightarrow{OM}$•$\overrightarrow{ON}$=-1计算可知直线MN恒过点(0,1),其方程为y=kx+1,利用两点间距离公式可知|MN|=$\sqrt{{k}^{2}+1}$•$\sqrt{4{k}^{2}+8}$,通过过M点的切线方程y-yM=xM(x-xM)与过N点的切线方程y-yN=xN(x-xN)作差、整理可知过M、N的两条抛物线的切线相交于点P(k,-1),
利用点到直线的距离公式可知点P到直线MN的距离d,利用S△PMN=$\frac{1}{2}$•d•|MN|计算即得结论.
解答 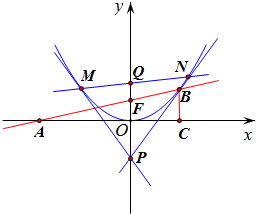 解:(1)过点B作x轴垂线交于C,则Rt△AOF~Rt△ACB,
解:(1)过点B作x轴垂线交于C,则Rt△AOF~Rt△ACB,
∵$\overrightarrow{AF}$=2$\overrightarrow{FB}$,∴$\frac{|AO|}{|AC|}$=$\frac{|OF|}{|CB|}$=$\frac{|AF|}{|AB|}$=$\frac{2}{3}$,
∵A(-$\sqrt{6}$,0),F(0,$\frac{p}{2}$),
∴xB+$\sqrt{6}$=$\frac{3}{2}$•$\sqrt{6}$,yB=$\frac{3}{2}$•$\frac{p}{2}$=$\frac{{{x}_{B}}^{2}}{2p}$,
解得:p=1,
∴抛物线的方程为:x2=2y;
(2)依题意,设直线MN的方程为:y=kx+b,
联立$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}=2y}\end{array}\right.$,消去y、整理得:x2-2kx-2b=0,
∴xMxN=-2b,xM+xN=2k,
∵$\overrightarrow{OM}$•$\overrightarrow{ON}$=-1,∴xMxN+yMyN=-1,
∴xMxN+$\frac{1}{4}$(xMxN)2=-1,
整理得:($\frac{1}{2}$xMxN+1)2=0,
解得:xMxN=-2,
∴-2b=-2,即b=1,
∴直线MN恒过点(0,1),其方程为y=kx+1,
且|MN|=$\sqrt{({x}_{M}-{x}_{N})^{2}+({y}_{M}-{y}_{N})^{2}}$
=$\sqrt{{k}^{2}+1}$•$\sqrt{({x}_{M}+{x}_{N})^{2}-4{x}_{M}{x}_{N}}$
=$\sqrt{{k}^{2}+1}$•$\sqrt{4{k}^{2}+8}$,
∵抛物线的方程为x2=2y,∴y′=x,
∴过M点的切线方程为:y-yM=xM(x-xM)=xMx-${{x}_{M}}^{2}$,即y=xMx-yM,
过N点的切线方程为:y-yN=xN(x-xN)=xNx-${{x}_{N}}^{2}$,即y=xNx-yN,
两式相减得:x=$\frac{{y}_{M}-{y}_{N}}{{{x}_{M}-x}_{N}}$=$\frac{\frac{1}{2}{{x}_{M}}^{2}-\frac{1}{2}{{x}_{N}}^{2}}{{x}_{M}-{x}_{N}}$=$\frac{1}{2}$(xM+xN)=$\frac{1}{2}•2k$=k,
∴y=xMx-yM=xM•$\frac{1}{2}$(xM+xN)-$\frac{1}{2}$${{x}_{M}}^{2}$=$\frac{1}{2}$xMxN=-1,
∴过M、N的两条抛物线的切线相交于点P(k,-1),
∵点P到直线MN的距离d=$\frac{|{k}^{2}+1+1|}{\sqrt{{k}^{2}+1}}$=$\frac{{k}^{2}+2}{\sqrt{{k}^{2}+1}}$,
∴S△PMN=$\frac{1}{2}$•d•|MN|
=$\frac{1}{2}$•$\frac{{k}^{2}+2}{\sqrt{{k}^{2}+1}}$•$\sqrt{{k}^{2}+1}$•$\sqrt{4{k}^{2}+8}$
=(k2+2)•$\sqrt{{k}^{2}+2}$
=$({k}^{2}+2)^{\frac{3}{2}}$,
显然当k=0时,△PMN面积的最小,最小值为${2}^{\frac{3}{2}}$=2$\sqrt{2}$.
点评 本题考查抛物线的简单性质,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 最大值为$-\frac{5}{3}$,最小值为$-\frac{5}{2}$ | B. | 最大值为$-\frac{5}{3}$,最小值不存在 | ||
| C. | 最大值为-2,最小值不存在 | D. | 最大值不存在,最小值为$-\frac{5}{2}$ |
| A. | ($\frac{1}{4}$,1+$\frac{\sqrt{2}}{2}$] | B. | ($\frac{1}{4}$,1] | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
| A. | 216 | B. | 288 | C. | 312 | D. | 360 |
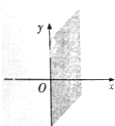 用弧度制表示终边落在阴影区域内角的集合{α|-$\frac{π}{2}$+2kπ≤α≤$\frac{π}{2}$+2kπ,k∈Z}.
用弧度制表示终边落在阴影区域内角的集合{α|-$\frac{π}{2}$+2kπ≤α≤$\frac{π}{2}$+2kπ,k∈Z}.