题目内容
1.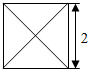 已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
分析 根据几何体的三视图,得出该几何体是底面为正方形的正四棱锥,结合图中数据求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体是底面边长为2的正方形,斜高为2的四棱锥,
且四棱锥的高为$\sqrt{{2}^{2}{-1}^{2}}$=$\sqrt{3}$的正四棱锥.
∴它的体积为V=$\frac{1}{3}$×22×$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查了利用空间几何体的三视图求体积的问题,也考查了空间想象能力的应用问题,是基础题目.

练习册系列答案
相关题目
11.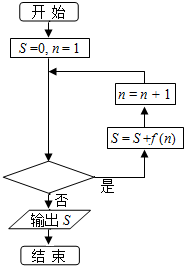 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )| A. | n≤100? | B. | n≤99? | C. | n>100? | D. | n>99? |
9.已知命题p:函数f(x)=sinxcosx的单调递增区间[$kπ-\frac{π}{4}$,$kπ+\frac{π}{4}$](k∈Z);命题q:函数g(x)=sin(x+$\frac{π}{2}$) 的图象关于原点对称,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∨q | C. | -p | D. | (-p)∨q |
16.函数f(x)=$\left\{\begin{array}{l}2x,0≤x≤1\\ 1,1<x<2\\ 3,x≥2\end{array}$的值域是( )
| A. | R | B. | [0,2]∪{3} | C. | [0,+∞) | D. | [-3,3] |
13.定义在(0,+∞)上的函数f(x)满足:?x∈(0,+∞),2f(x)<xf′(x)<3f(x)恒成立,其中f′(x)为f(x)的导函数,则( )
| A. | $\frac{1}{16}$<$\frac{f(1)}{f(2)}$<$\frac{1}{8}$ | B. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ | C. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{3}$ | D. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ |
10.若圆C1的方程是x2+y2-4x-4y+7=0,圆C2的方程为x2+y2-4x-10y+13=0,则两圆的公切线有( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 1条 |
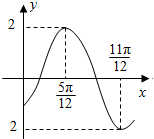 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是-$\sqrt{3}$.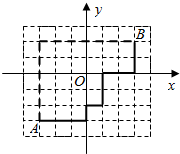 现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.