题目内容
10.若圆C1的方程是x2+y2-4x-4y+7=0,圆C2的方程为x2+y2-4x-10y+13=0,则两圆的公切线有( )| A. | 2条 | B. | 3条 | C. | 4条 | D. | 1条 |
分析 把两圆的方程化为标准形式,分别求出圆心和半径,考查两圆的圆心距正好等于两圆的半径之差,故两圆相内切.推出公切线的条数.
解答 解:圆C1的方程即:(x-2)2+(y-2)2=1,圆心C1(2,2),半径 为1,
圆C2的方程即:(x-2)2+(y-5)2=16,圆心C2(2,5),半径 为4,
两圆的圆心距为$\sqrt{{(2-2)}^{2}+{(5-2)}^{2}}$=3,正好等于两圆的半径之差,故两圆相内切,故两圆的公切线有1条,
故选:D.
点评 本题考查两圆的位置关系,两圆相外切的充要条件是:两圆的圆心距等于两圆的半径之和;两圆相外切时,公切线3条.考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知定义在R上的奇函数f(x),满足2016f(-x)<f′(x)恒成立,且f(1)=e-2016,则下列结论正确的是( )
| A. | f(2016)<0 | B. | f(2016)<e${\;}^{-201{6}^{2}}$ | ||
| C. | f(2)<0 | D. | f(2)>e-4032 |
15.将函数f(x)=sin2x的图象向左平移$\frac{π}{12}$个单位,得到函数g(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)的图象,则φ等于$\frac{π}{6}$.
2.sin70°cos10°+cos110°sin10°=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
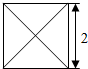 已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.