题目内容
(本小题共14分)
已知椭圆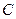 的焦点是
的焦点是 ,
, ,点
,点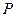 在椭圆上且满足
在椭圆上且满足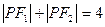 .
.
(Ⅰ)求椭圆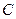 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆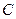 的交点为
的交点为 ,
,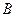 .
.
(i)求使 的面积为
的面积为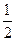 的点
的点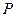 的个数;
的个数;
(ii)设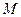 为椭圆上任一点,
为椭圆上任一点, 为坐标原点,
为坐标原点, ,求
,求 的值.
的值.
已知椭圆
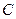 的焦点是
的焦点是 ,
, ,点
,点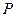 在椭圆上且满足
在椭圆上且满足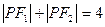 .
.(Ⅰ)求椭圆
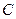 的标准方程;
的标准方程;(Ⅱ)设直线
 与椭圆
与椭圆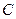 的交点为
的交点为 ,
,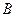 .
.(i)求使
 的面积为
的面积为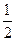 的点
的点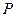 的个数;
的个数;(ii)设
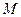 为椭圆上任一点,
为椭圆上任一点, 为坐标原点,
为坐标原点, ,求
,求 的值.
的值.(Ⅰ)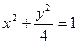 (Ⅱ)(i)符合条件的点
(Ⅱ)(i)符合条件的点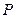 有2个(ii)
有2个(ii)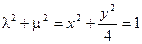
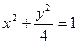 (Ⅱ)(i)符合条件的点
(Ⅱ)(i)符合条件的点 有2个(ii)
有2个(ii)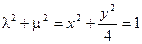
(Ⅰ)∵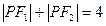 >
>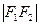
∴点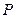 满足的曲线
满足的曲线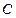 的方程为椭圆
的方程为椭圆
∵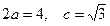
∴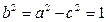
∴椭圆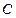 的标准方程为
的标准方程为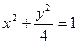 . …………4分
. …………4分
(Ⅱ)(i)∵ 直线 与椭圆
与椭圆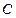 的交点为
的交点为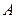 ,
,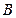
∴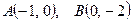 ,
,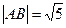
若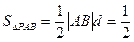
∴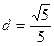
∵原点 到直线
到直线 的距离是
的距离是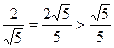
∴在直线 的右侧有两个符合条件的
的右侧有两个符合条件的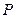 点
点
设直线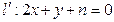 与椭圆相切,则
与椭圆相切,则
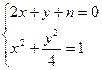 有且只有一个交点
有且只有一个交点
∴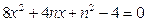 有且只有一个解
有且只有一个解
由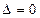 解得
解得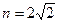 (设负)
(设负)
此时,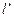 与
与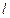 间距离为
间距离为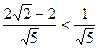
∴在直线 的左侧不存在符合条件的
的左侧不存在符合条件的 点
点
∴符合条件的点 有2个. ………………10分
有2个. ………………10分
(ii)设 ,则
,则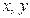 满足方程:
满足方程: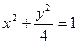
∵
∴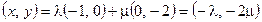
即: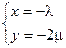 ,从而有
,从而有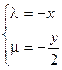
∴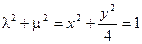 . ……………14分
. ……………14分
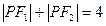 >
>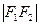
∴点
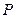 满足的曲线
满足的曲线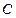 的方程为椭圆
的方程为椭圆∵
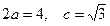
∴
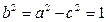
∴椭圆
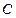 的标准方程为
的标准方程为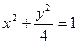 . …………4分
. …………4分(Ⅱ)(i)∵ 直线
 与椭圆
与椭圆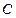 的交点为
的交点为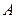 ,
,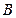
∴
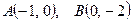 ,
,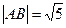
若
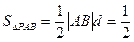
∴
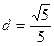
∵原点
 到直线
到直线 的距离是
的距离是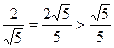
∴在直线
 的右侧有两个符合条件的
的右侧有两个符合条件的 点
点设直线
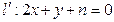 与椭圆相切,则
与椭圆相切,则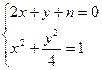 有且只有一个交点
有且只有一个交点∴
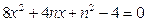 有且只有一个解
有且只有一个解由
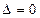 解得
解得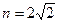 (设负)
(设负)此时,
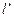 与
与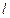 间距离为
间距离为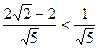
∴在直线
 的左侧不存在符合条件的
的左侧不存在符合条件的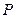 点
点∴符合条件的点
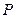 有2个. ………………10分
有2个. ………………10分(ii)设
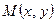 ,则
,则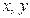 满足方程:
满足方程: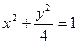
∵

∴
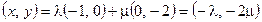
即:
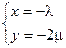 ,从而有
,从而有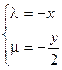
∴
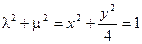 . ……………14分
. ……………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
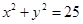 ,过
,过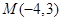 作直线
作直线 与圆交于点
与圆交于点 ,且
,且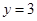 对称,则直线
对称,则直线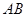 的斜率等于
的斜率等于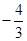
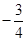
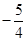
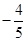
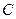 :
: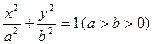 的离心率为
的离心率为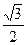 ,过坐标原点
,过坐标原点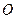 且斜率为
且斜率为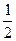 的直线
的直线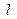 与
与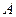 、
、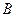 ,
,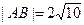 .
.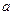 、
、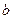 的值;
的值;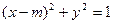 与椭圆
与椭圆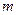 的取值范围.
的取值范围.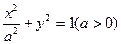 与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。
与x轴的左右两个交点,直线l过点B且x轴垂直,M为l上的一点,连结AM交曲线C于点T。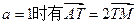 ,求点T坐标;
,求点T坐标;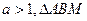 的面积为2,当
的面积为2,当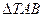 的面积的最大值为
的面积的最大值为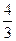 时,求曲线C的离心率e的取值范围。
时,求曲线C的离心率e的取值范围。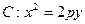 ,过点
,过点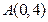 的直线
的直线 交抛物线
交抛物线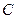 于
于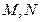 两点,且
两点,且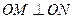 .
.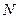 作
作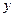 轴的平行线与直线
轴的平行线与直线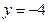 相交于点
相交于点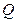 ,若
,若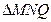 是等腰三角形,求直线
是等腰三角形,求直线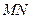 的方程.
的方程.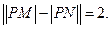
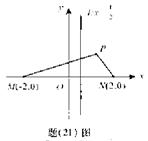
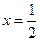 的距离,若
的距离,若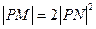 ,求
,求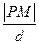 的值.
的值. 的左
的左 、右焦点为F1、F2,其一条渐近线为y=x,点P
、右焦点为F1、F2,其一条渐近线为y=x,点P 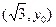 在该双曲线上,则
在该双曲线上,则 =( )
=( )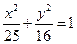 的焦点为
的焦点为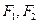 ,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 。
,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 。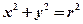 ,经过圆上一点
,经过圆上一点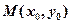 的切线方程为
的切线方程为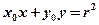 ,类比上述方法可以得到椭圆
,类比上述方法可以得到椭圆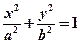 类似的性质为________。
类似的性质为________。