题目内容
已知双曲线 的左
的左 、右焦点为F1、F2,其一条渐近线为y=x,点P
、右焦点为F1、F2,其一条渐近线为y=x,点P 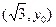 在该双曲线上,则
在该双曲线上,则 =( )
=( )
 的左
的左 、右焦点为F1、F2,其一条渐近线为y=x,点P
、右焦点为F1、F2,其一条渐近线为y=x,点P 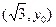 在该双曲线上,则
在该双曲线上,则 =( )
=( )| A.-12 | B.-2 | C.0 | D.4 |
C
略

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
题目内容
 的左
的左 、右焦点为F1、F2,其一条渐近线为y=x,点P
、右焦点为F1、F2,其一条渐近线为y=x,点P 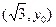 在该双曲线上,则
在该双曲线上,则 =( )
=( )| A.-12 | B.-2 | C.0 | D.4 |

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案