题目内容
已知椭圆C1: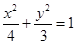 ,抛物线C2:
,抛物线C2: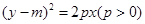 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅰ)当AB⊥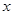 轴时,求
轴时,求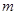 、
、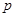 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在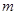 、
、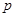 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的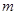 、
、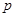 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
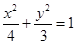 ,抛物线C2:
,抛物线C2: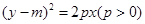 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.(Ⅰ)当AB⊥
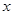 轴时,求
轴时,求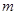 、
、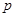 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;(Ⅱ)是否存在
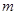 、
、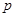 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的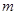 、
、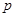 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(Ⅰ)m=0, 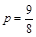 .此时C2的焦点坐标为(
.此时C2的焦点坐标为(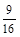 ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(II)满足条件的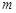 、
、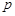 存在,且
存在,且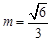 或
或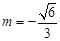 ,
,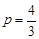 .
.
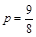 .此时C2的焦点坐标为(
.此时C2的焦点坐标为(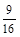 ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.(II)满足条件的
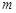 、
、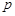 存在,且
存在,且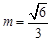 或
或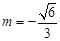 ,
,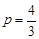 .
.试题分析:(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为: x =1,从而点A的坐标为(1,
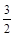 )或(1,-
)或(1,-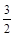 ). 因为点A在抛物线上.所以
). 因为点A在抛物线上.所以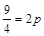 ,即
,即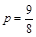 .此时C2的焦点坐标为(
.此时C2的焦点坐标为(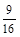 ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.(II): 假设存在
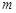 、
、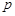 的值使
的值使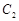 的焦点恰在直线AB上,由(I)知直线AB的斜率存在,故可设直线AB的方程为
的焦点恰在直线AB上,由(I)知直线AB的斜率存在,故可设直线AB的方程为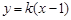 .
.由
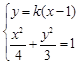 消去
消去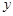 得
得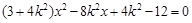 …①
…①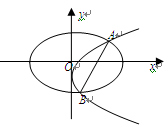
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程①的两根,x1+x2=
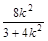 .
.由
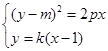 消去y得
消去y得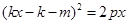 . ………………②
. ………………②因为C2的焦点
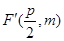 在直线
在直线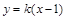 上,
上,所以
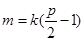 ,即
,即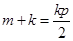 .代入②有
.代入②有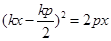 .
.即
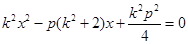 . …………………③
. …………………③由于x1,x2也是方程③的两根,所以x1+x2=
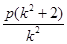 .
.从而
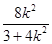 =
=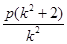 . 解得
. 解得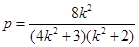 ……………………④
……………………④又AB过C1,C2的焦点,所以
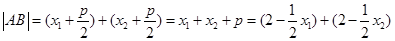 ,
,则
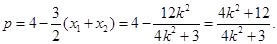 …………………………………⑤
…………………………………⑤由④、⑤式得
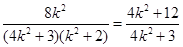 ,即
,即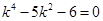 .
.解得
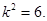 于是
于是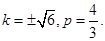
因为C2的焦点
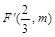 在直线
在直线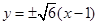 上,所以
上,所以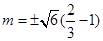 .
.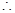
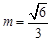 或
或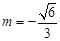 .
.由上知,满足条件的
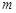 、
、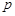 存在,且
存在,且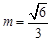 或
或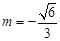 ,
,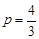 .
.点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题解答过程中,主要运用了抛物线的几何性质。结合抛物线的焦半径公式,建立了k的方程。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
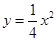 的焦点坐标是
的焦点坐标是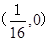
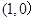
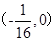
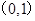
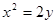 上任意一点
上任意一点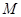 向圆
向圆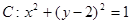 作切线
作切线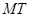 ,则切线长
,则切线长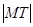 的最小值为
的最小值为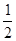
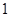
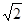
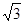
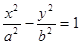 的左、右焦点.若双曲线上存在点A,使
的左、右焦点.若双曲线上存在点A,使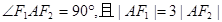 ,则双曲线的离心率为( )
,则双曲线的离心率为( )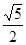
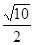

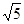
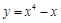 上点
上点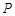 处的切线平行于直线
处的切线平行于直线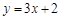 ,那么点
,那么点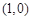
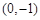
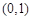
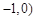
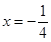

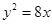 的焦点,M的离心率
的焦点,M的离心率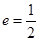 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线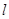 ,交M于A,B两点。
,交M于A,B两点。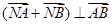 ,求实数t的取值范围。
,求实数t的取值范围。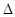
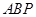 的顶点
的顶点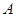 、
、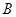 分别为双曲线
分别为双曲线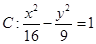 的左右焦点,顶点
的左右焦点,顶点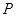 在双曲线
在双曲线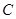 上,则
上,则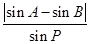 的值等于
的值等于 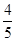
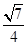
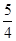
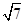
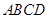 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛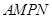 ,要求
,要求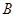 点在
点在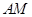 上,
上, 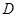 点在
点在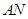 上,且对角线
上,且对角线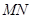 过点
过点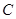 ,已知
,已知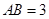 米,
米,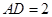 米.
米.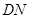 的长应在什么范围内?
的长应在什么范围内?