题目内容
(本小题满分12分)
如图所示,将一矩形花坛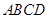 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛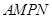 ,要求
,要求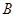 点在
点在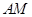 上,
上, 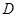 点在
点在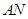 上,且对角线
上,且对角线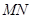 过点
过点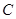 ,已知
,已知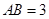 米,
米,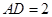 米.
米.
(1)要使矩形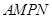 的面积大于32平方米,则
的面积大于32平方米,则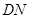 的长应在什么范围内?
的长应在什么范围内?
(2)当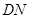 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛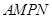 的面积最小?并求出最小值.
的面积最小?并求出最小值.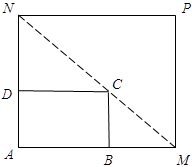
如图所示,将一矩形花坛
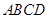 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛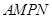 ,要求
,要求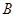 点在
点在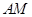 上,
上, 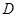 点在
点在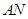 上,且对角线
上,且对角线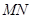 过点
过点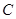 ,已知
,已知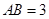 米,
米,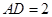 米.
米.(1)要使矩形
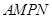 的面积大于32平方米,则
的面积大于32平方米,则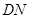 的长应在什么范围内?
的长应在什么范围内?(2)当
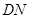 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛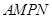 的面积最小?并求出最小值.
的面积最小?并求出最小值.
(1)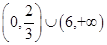 (2)当且仅当
(2)当且仅当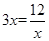 即
即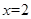 时,矩形花坛的面积最小为24平方米
时,矩形花坛的面积最小为24平方米
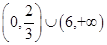 (2)当且仅当
(2)当且仅当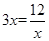 即
即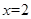 时,矩形花坛的面积最小为24平方米
时,矩形花坛的面积最小为24平方米试题分析:解:设
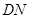 的长为
的长为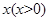 米,则
米,则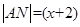 米,
米,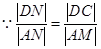
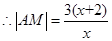
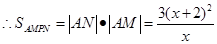 …………………3分
…………………3分由
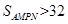 得
得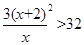
又
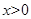 得
得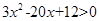
解得:
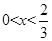 或
或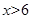
即
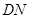 的长的取值范围是
的长的取值范围是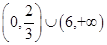 …………………6分
…………………6分(2)矩形花坛的面积为:
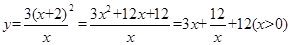
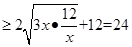 …………………11分
…………………11分当且仅当
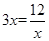 即
即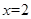 时,矩形花坛的面积最小为24平方米. …………………12分
时,矩形花坛的面积最小为24平方米. …………………12分点评:通过对于已知中相似的理解,得到所求的面积公式,然后结合实际的背景得到变量的范围, 同时解决均值不等式的思想来求解最值。属于中档题。

练习册系列答案
相关题目
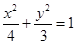 ,抛物线C2:
,抛物线C2: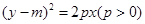 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.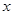 轴时,求
轴时,求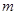 、
、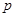 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;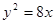 的焦点为
的焦点为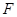 ,准线为
,准线为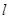 ,
,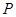 为抛物线上的一点,
为抛物线上的一点,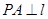 ,垂足为
,垂足为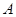 .若直线
.若直线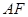 的斜率为
的斜率为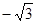 ,则
,则
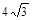
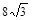
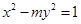 的实轴长是虚轴长的2倍,则rn=
的实轴长是虚轴长的2倍,则rn=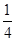
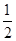
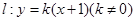 与椭圆
与椭圆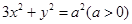 相交于
相交于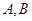 两个不同的点,与
两个不同的点,与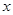 轴相交于点
轴相交于点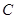 ,记
,记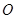 为坐标原点.
为坐标原点.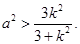
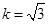 且
且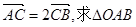 的面积及椭圆方程.
的面积及椭圆方程.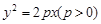 的焦点在圆
的焦点在圆 上,则
上,则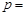 .
.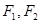 是椭圆
是椭圆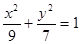 的两个焦点,
的两个焦点,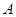 为椭圆上的一点,且
为椭圆上的一点,且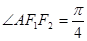 ,则
,则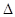
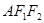 的面积是( )
的面积是( )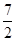
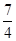
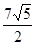
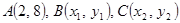 在抛物线
在抛物线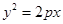 上,
上,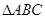 的重心与此抛物线的焦点F重合。
的重心与此抛物线的焦点F重合。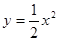 上的动点,点P在x轴上的射影为M,点A的坐标是
上的动点,点P在x轴上的射影为M,点A的坐标是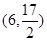 ,则
,则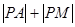 的最小值是( )
的最小值是( )