题目内容
11.已知数列{an}满足an+1=an-$\frac{1}{n(n+1)}$,a1=3,数列{bn}的前n项和Sn=-$\frac{1}{2}$n2-$\frac{401}{2}$n+1(1)求数列{an},{bn}的通项公式;
(2)设cn=$\frac{1}{{a}_{n}•{b}_{n}}$,求数列{cn}的最小项.
分析 (1)通过an+1-an=$\frac{1}{n+1}$-$\frac{1}{n}$,并项累加即得数列{an}的通项,利用bn+1=Sn+1-Sn及b1=-200,可得数列{bn}的通项;
(2)通过当n≥2时,利用基本不等式可得an•bn=-401-(2n+$\frac{200}{n}$)≤-441,进而可得结论.
解答 解:(1)∵an+1=an-$\frac{1}{n(n+1)}$,
∴an+1-an=-$\frac{1}{n(n+1)}$=$\frac{1}{n+1}$-$\frac{1}{n}$,
累加可得:an-a1=$\frac{1}{n}$-1,
∴an=a1+$\frac{1}{n}$-1=2+$\frac{1}{n}$,
即数列{an}的通项为:an=2+$\frac{1}{n}$;
∵Sn=-$\frac{1}{2}$n2-$\frac{401}{2}$n+1,
∴Sn+1=-$\frac{1}{2}$(n+1)2-$\frac{401}{2}$(n+1)+1,
两式相减得:bn+1=Sn+1-Sn
=[-$\frac{1}{2}$(n+1)2-$\frac{401}{2}$(n+1)+1]-[-$\frac{1}{2}$n2-$\frac{401}{2}$n+1]
=-n-201,
即bn+1=-(n+1)-200,
又b1=-$\frac{1}{2}$-$\frac{401}{2}$+1=-200,
∴数列{bn}的通项为:bn=$\left\{\begin{array}{l}{-200,}&{n=1}\\{-200-n,}&{n≥2}\end{array}\right.$;
(2)∵cn=$\frac{1}{{a}_{n}•{b}_{n}}$,∴c1=$\frac{1}{{a}_{1}•{b}_{1}}$=$\frac{1}{3•(-200)}$=-$\frac{1}{600}$;
当n≥2时,an•bn=(2+$\frac{1}{n}$)•(-200-n)=-401-(2n+$\frac{200}{n}$),
∵2n+$\frac{200}{n}$≥2$\sqrt{2n•\frac{200}{n}}$=40(当且仅当2n=$\frac{200}{n}$即n=10时等号成立),
∴an•bn≤-401-40=-441,
∴cn=$\frac{1}{{a}_{n}•{b}_{n}}$≥-$\frac{1}{441}$(当且仅当n=10时等号成立),
∴数列{cn}的最小项为:c10.
点评 本题考查求数列的通项,考查运算求解能力,考查基本不等式,注意解题方法的积累,属于中档题.

| A. | -2i | B. | 2i | C. | -i | D. | i |

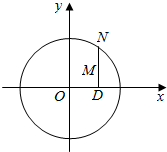 如图所示,点N在圆O:x2+y2=8上,点D是N在x轴上投影,M为DN上一点,且满足$\overrightarrow{DN}$=$\sqrt{2}$$\overrightarrow{DM}$.
如图所示,点N在圆O:x2+y2=8上,点D是N在x轴上投影,M为DN上一点,且满足$\overrightarrow{DN}$=$\sqrt{2}$$\overrightarrow{DM}$.