题目内容
3．用6种不同的颜色给下列三个图中的4个格子涂色，每个格子涂一种颜色，且要求相邻的两个格子颜色不同，则
（1）图1和图2中不同的涂色方法分别有多少种？
（2）图3最多只能使用3种颜色，不同的涂色方法有多少种？
分析 （1）图1中，A有6种涂色方法，B种有5种涂色方法，C有4种涂色方法，D有5种涂色方法，所以根据分步计数原理知答案；
图2中，分若A，D同色，若A，D异色，根据分类计数原理知答案；
（2）分用2色涂格子，和用3色涂格子，需要先选色再涂色．
解答 解：如图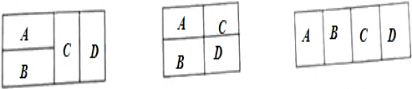
（1）图1中，A有6种涂色方法，B种有5种涂色方法，C有4种涂色方法，D有5种涂色方法，
所以根据分步计数原理知共有6×5×4×5=600种涂法，
图2中，若A，D同色，A有6种涂色方法，B种有5种涂色方法，C有5种涂色方法，故有6×5×5=150种，
若A，D异色，A有6种涂色方法，D有5种涂色方法，B种4种涂色方法，C有4种涂色方法，6×5×4×4=480，
所以根据分类计数原理知共有150+480=630种涂法，
（2）用2色涂格子有C62×2=30种方法，
用3色涂格子，第一步选色有C63，第二步涂色，共有3×2（1×1+1×2）=18种，
所以涂色方法18×C63=360种方法，
故总共有390种方法．
点评 本题考查计数原理的应用，本题解题的关键是分析题目时时要按一定顺序，由相邻情况来确定可以涂色的情况数目，最后根据分步或分类计数原理得到结果．
练习册系列答案
相关题目
如图，在空间四边形ABCD中，AB=CD=8，M，N分别是BC，AD的中点，若异面直线AB与CD所成的角为60°时，求MN的长．