题目内容
2.已知i是虚数单位,则i3+$\frac{1}{i}$=( )| A. | -2i | B. | 2i | C. | -i | D. | i |
分析 利用复数的运算法则即可得出.
解答 解:i3+$\frac{1}{i}$=-i+$\frac{-i}{-i•i}$=-2i=-2i.
故选:A.
点评 本题考查了复数的运算法则,属于基础题.

练习册系列答案
相关题目
13.某校对数学、物理两科进行学业水平考前辅导,辅导后进行测试,按成绩(满分100分)划分为合格(成绩大于或等于70分)和不合格(成绩小于70分).现随机抽取两科各100名学生的成绩统计如下:
(1)试分别估计该校学生数学、物理合格的概率;
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
17.已知实数x,y满足条件$\left\{\begin{array}{l}2x+y≥4\\ x-y≥1\\ x-2y≤2\end{array}\right.$,则z=x+2y的最小值为( )
| A. | $\frac{4}{3}$ | B. | 4 | C. | 2 | D. | 3 |
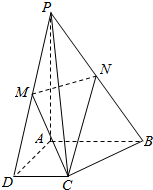 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.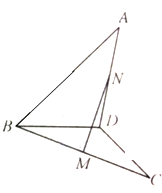 如图,在空间四边形ABCD中,AB=CD=8,M,N分别是BC,AD的中点,若异面直线AB与CD所成的角为60°时,求MN的长.
如图,在空间四边形ABCD中,AB=CD=8,M,N分别是BC,AD的中点,若异面直线AB与CD所成的角为60°时,求MN的长.