题目内容
6.设f(x)是偶函数,且当x≥0时,f(x)=$\left\{\begin{array}{l}x(3-x),0≤x≤3\\(x-3)(a-x),x>3\end{array}$.(1)当a=5时,判断f(x)=1有几个不同的实数根,说明理由;
(2)设函数f(x)在区间[-5,5]上最大值为g(a),试求g(a)的表达式;
(3)若方程f(x)=m恰有四个不同的实根x1,x2,x3,x4,x1<x2<x3<x4,且它们依次构成等差数列,求a的取值范围及m的值.
分析 (1)将a=5代入f(x)=$\left\{\begin{array}{l}x(3-x),0≤x≤3\\(x-3)(a-x),x>3\end{array}$,可求出f(x)=1的正根,进而根据f(x)是偶函数得到对应的负根;
(2)因为f(x)是偶函数,所以它在区间[-5,5]上的最大值即为它在区间[0,5]上的最大值,分类讨论,即可求得结论;
(3)设这四个根从小到大依次为x1,x2,x3,x4,则当方程f(x)=m在[-3,3]上有四个实根时,由x4-x3=2x3,且x4+x3=3,得x3=$\frac{3}{4}$,x4=$\frac{9}{4}$,从而m=f($\frac{3}{4}$)=$\frac{27}{16}$,且要求f(x)<$\frac{27}{16}$对x∈(3,+∞)恒成立,由此可得结论.
解答 解:(1)当0≤x≤3时,解f(x)=x(3-x)=1得:x=$\frac{3-\sqrt{5}}{2}$,或x=$\frac{3+\sqrt{5}}{2}$…(2分)
当x>3,a=5时,f(x)=(x-3)(5-x)=1得:x=4,
故x≥0时,f(x)=1有三个正根,
又∵f(x)是偶函数,
∴x≤0时,f(x)=1有三个负根,
综上f(x)=1有六个根,(4分)
(2)因为f(x)是偶函数,所以它在区间[-5,5]上的最大值即为它在区间[0,5]上的最大值,
①当a≤3时,f(x)在[0,$\frac{3}{2}$]上单调递增,在[$\frac{3}{2}$,+∞)上单调递减,所以g(a)=f($\frac{3}{2}$)=$\frac{9}{4}$…(5分)
②当3<a≤7时,f(x)在[0,$\frac{3}{2}$]与[3,$\frac{3+a}{2}$]上单调递增,在[$\frac{3}{2}$,3]与[$\frac{3+a}{2}$,5]上单调递减,
所以此时只需比较f($\frac{3}{2}$)=$\frac{9}{4}$与f($\frac{3+a}{2}$)=$\frac{(a-3)^{2}}{4}$的大小.
1°当3<a≤6时,f($\frac{3}{2}$)=$\frac{9}{4}$≥f($\frac{3+a}{2}$)=$\frac{(a-3)^{2}}{4}$,所以g(a)=f($\frac{3}{2}$)=$\frac{9}{4}$…(6分)
2°当6<a≤7时,f($\frac{3}{2}$)=$\frac{9}{4}$<f($\frac{3+a}{2}$)=$\frac{(a-3)^{2}}{4}$,所以g(a)=f($\frac{3+a}{2}$)=$\frac{(a-3)^{2}}{4}$…(7分)
3°当a>7时,f(x)在[0,$\frac{3}{2}$]与[3,5]上单调递增,在[$\frac{3}{2}$,3]上单调递减,且f($\frac{3}{2}$)=$\frac{9}{4}$<f(5)=2(a-5),所以g(a)=f(5)=2(a-5)…(8分)
综上所述,g(a)=$\left\{\begin{array}{l}\frac{9}{4},a≤6\\ \frac{(a-3)^{2}}{4},6<a≤7\\ 2(a-5),a>7\end{array}\right.$ …(9分)
(3)设这四个根从小到大依次为x1,x2,x3,x4.
当方程f(x)=m在[-3,3]上有四个实根时,由x4-x3=2x3,且x4+x3=3,得x3=$\frac{3}{4}$,x4=$\frac{9}{4}$从而m=f($\frac{3}{4}$)=$\frac{27}{16}$,且要求f(x)<$\frac{27}{16}$对x∈(3,+∞)恒成立…(10分)
1°当a≤3时,f(x)在(3,+∞)上单调递减,所以f(x)<f(3)=0<$\frac{27}{16}$对x∈(3,+∞)恒成立,即a≤3适合题意…(11分)
2°当a>3时,欲f(x)<$\frac{27}{16}$对x∈(3,+∞)恒成立,只要f($\frac{3+a}{2}$)=$\frac{(a-3)^{2}}{4}$<$\frac{27}{16}$,解得a<3+$\frac{3\sqrt{3}}{2}$,故此时应满足3<a<3+$\frac{3\sqrt{3}}{2}$…(12分)
综上所述,a与m满足的条件为m=$\frac{27}{16}$且a<3+$\frac{3\sqrt{3}}{2}$.
点评 本题考查函数解析式的确定,考查函数的最值,考查分类讨论的数学思想,考查数列与函数的结合,属于中档题.

| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
| A. | $\frac{4}{3}$ | B. | 4 | C. | 2 | D. | 3 |
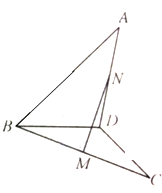 如图,在空间四边形ABCD中,AB=CD=8,M,N分别是BC,AD的中点,若异面直线AB与CD所成的角为60°时,求MN的长.
如图,在空间四边形ABCD中,AB=CD=8,M,N分别是BC,AD的中点,若异面直线AB与CD所成的角为60°时,求MN的长. 某同学做了一个如图所示的等腰直角三角形形状的数表,且把奇数和偶数分别依次排在了数表的奇数行和偶数行,若用a(i,j)表示第i行从左数第j个数,如a(4,3)=10,则a(21,6)=( )
某同学做了一个如图所示的等腰直角三角形形状的数表,且把奇数和偶数分别依次排在了数表的奇数行和偶数行,若用a(i,j)表示第i行从左数第j个数,如a(4,3)=10,则a(21,6)=( )