题目内容
19.由直线y=0,x=e,y=2x及曲线y=$\frac{2}{x}$所围成的封闭的图形的面积为3.分析 首先由题意画出图形,明确围成的封闭图形用定积分表示,然后求定积分.
解答 解:由题意,直线y=0,x=e,y=2x及曲线y=$\frac{2}{x}$所围成的封闭的图形如图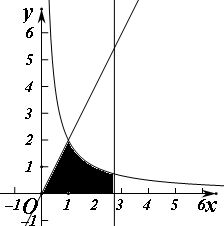
直线y=2x与曲线y=$\frac{2}{x}$的交点为(1,2),
所以阴影部分的面积为:${∫}_{0}^{1}2xdx+{∫}_{1}^{e}\frac{2}{x}dx$=x2|${\;}_{0}^{1}$+2lnx|${\;}_{1}^{e}$=3;
故答案为:3.
点评 本题考查了利用定积分求曲边梯形的面积;关键是明确被积函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知全集U=R,集合A={x|y=log3(x-1)},B={y|y=2x},则(∁∪A)∩B=( )
| A. | (0,+∞) | B. | (0,1] | C. | (1,+∞) | D. | (1,2) |
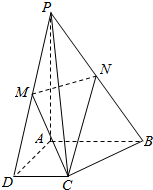 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.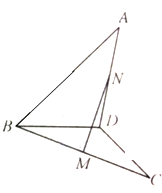 如图,在空间四边形ABCD中,AB=CD=8,M,N分别是BC,AD的中点,若异面直线AB与CD所成的角为60°时,求MN的长.
如图,在空间四边形ABCD中,AB=CD=8,M,N分别是BC,AD的中点,若异面直线AB与CD所成的角为60°时,求MN的长.