题目内容
20. 如图所示,点N在圆O:x2+y2=8上,点D是N在x轴上投影,M为DN上一点,且满足$\overrightarrow{DN}$=$\sqrt{2}$$\overrightarrow{DM}$.
如图所示,点N在圆O:x2+y2=8上,点D是N在x轴上投影,M为DN上一点,且满足$\overrightarrow{DN}$=$\sqrt{2}$$\overrightarrow{DM}$.(Ⅰ)当点N在圆O上运动时,求点M的轨迹C的方程.
(Ⅱ)过F(2,0)不与坐标轴垂直的直线交曲线C于P,Q两点,线段PQ的垂直平分线交x轴于点E,试判断$\frac{|EF|}{|PQ|}$是否为定值?若是定值,求此定值;若不是定值,请说明理由.
分析 (Ⅰ)分别设出M,N的坐标,根据题意表示出N的坐标,代入圆的方程即可求得C的轨迹方程.
(Ⅱ)设出直线方程与圆的方程联立,利用韦达定理表示出y1+y2和y1y2,进而利用弦长公式表示出|PQ|,利用弦PQ的中点,表示出其垂直平分线的方程,把y=0带入求得横坐标的表达式,进而表示出|FE|,相除即可.
解答 解:(Ⅰ)设M(x,y)、N(x0,y0),由于$\overrightarrow{DN}$=$\sqrt{2}$$\overrightarrow{DM}$和ND⊥x轴,
所以$\left\{\begin{array}{l}{x={x}_{0}}\\{{y}_{0}=\sqrt{2}y}\end{array}\right.$
代入圆方程得:x2+2y2=8,即$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.
所以,曲线C的轨迹方程为即$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.
(Ⅱ)$\frac{|EF|}{|PQ|}$是定值,值为$\frac{\sqrt{2}}{4}$.理由如下:
由题设直线x=my+2(m≠0)交曲线C:x2+2y2=8于P(x1,y1),Q(x2,y2)联立得$\left\{\begin{array}{l}{x=my+2}\\{{x}^{2}+2{y}^{2}-8=0}\end{array}\right.$得(m2+2)y2+4my-4=0,则y1+y2=-$\frac{4m}{{m}^{2}+2}$,y1y2=$\frac{-4}{{m}^{2}+2}$,
∴|PQ|=$\sqrt{1+{m}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{1+{m}^{2}}$•$\sqrt{(\frac{-4m}{{m}^{2}+2})^{2}+\frac{16}{{m}^{2}+2}}$=$\frac{4\sqrt{2}({m}^{2}+1)}{{m}^{2}+2}$,
弦PQ的中点为($\frac{4}{{m}^{2}+2}$,$\frac{-2m}{{m}^{2}+2}$),
∴直线x=my+2的垂直平分线方程为y-$\frac{-2m}{{m}^{2}+2}$=-m(x-$\frac{4}{{m}^{2}+2}$),
令y=0,得x=$\frac{2}{{m}^{2}+2}$,所以|FE|=2-$\frac{2}{{m}^{2}+2}$=$\frac{2({m}^{2}+1)}{{m}^{2}+2}$,
∴$\frac{|EF|}{|PQ|}$=$\frac{\sqrt{2}}{4}$
点评 本题主要考查了直线与圆的方程的综合运用问题.直线与圆的方程问题的解决常借助于韦达定理,利用设而不求的方法解决.

| A. | (0,+∞) | B. | (0,1] | C. | (1,+∞) | D. | (1,2) |
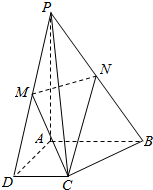 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.