题目内容
某食品厂对生产的某种食品按行业标准分成五个不同等级，等级系数X依次为A，B，C，D,E.现从该种食品中随机抽取20件样品进行检验，对其等级系数进行统计分析，得到频率分布表如下：
(1)在所抽取的20件样品中，等级系数为D的恰有3件，等级系数为E的恰有2件，求a,b,c的值；
(2)在（1)的条件下，将等级系数为D的3件样品记为x1，x2，x3，等级系数为E的2件样品记为y1，y2，现从x1，x2，x3，y1，y2这5件样品中一次性任取两件（假定每件样品被取出的可能性相同），试写出所有可能的结果，并求取出的两件样品是同一等级的概率．
（1）a＝0.1，b＝0.15，c＝0.1；（2）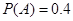
.
解析试题分析：本题主要考查频率分布表和随机事件的概率等数学知识，考查学生分析问题解决问题的能力和计算能力.第一问，利用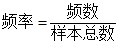
分别求出
和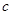
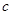的值，而由频率分布表知所有频率之和为1，利用上述所求的和，求出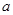
的值；第二问，列出在5件中任取2件的所有情况共10个，在这10个中选出同一等级的情况共4个，并求出概率.
试题解析：(1)由频率分布表得a＋0.2＋0.45＋b＋c＝1，即a＋b＋c＝0.35.
因为抽取的20件样品中，等级系数为D的恰有3件，所以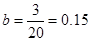
.
等级系数为E的恰有2件，所以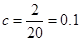
.
从而a＝0.35－b－c＝0.1.
所以a＝0.1，b＝0.15，c＝0.1.（6分）
(2)从样品x1，x2，x3，y1，y2中任取两件，所有可能的结果为：
(x1，x2)，(x1，x3)，(x1，y1)，(x1，y2)，(x2，x3)，(x2，y1)，(x2，y2)，(x3，y1)，(x3，y2)，(y1，y2)，共计10个．
设事件A表示“从样品x1，x2，x3，y1，y2中任取两件，其等级系数相等”，
则A包含的基本事件为：(x1，x2)，(x1，x3)，(x2，x3)，(y1，y2)，共4个．
故所求的概率
.（12分）
考点：1.频率分布表；2.频率的计算；3.随机事件的概率.
某公司生产产品A，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于
小于
为二等品，小于为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利
元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：
| 测试指标 |  |  |  |  |  |  |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率．
（1）计算新工人乙生产三件产品A，给工厂带来盈利大于或等于100元的概率；
（2）记甲乙分别生产一件产品A给工厂带来的盈利和记为X，求随机变量X的概率分布和数学期望．
一汽车厂生产
、
、
三类轿车，每类轿车均有舒适型和标准型两种型号,某月的产量如下表（单位：辆）
| | 轿车 | 轿车 | 轿车 |
| 舒适型 |  |  |  |
| 标准型 |  |  |  |
辆，其中有类轿车
辆.（1）求
的值；（2）用分层抽样的方法在
类轿车中抽取一个容量为
的样本.将该样本看成一个总体，从中任取
辆，求至少有
辆舒适型轿车的概率；（3）用随机抽样的方法从
类舒适型轿车中抽取
辆，经检测它们的得分如下：
、
、
、
、
、
、
、
.把这辆轿车的得分看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过
的概率. 某班主任对全班50名学生进行了作业量多少的调查．数据如下表：
| | 认为作业多 | 认为作业不多 | 合计 |
| 喜欢玩游戏 | 18 | 9 | |
| 不喜欢玩游戏 | 8 | 15 | |
| 合计 | | | |
（2）试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系？
附：
| P(K2≥K0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
