题目内容
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |  |  |  |  |  |  |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的概率;
(2)记甲乙分别生产一件产品A给工厂带来的盈利和记为X,求随机变量X的概率分布和数学期望.
(1) ;(2)
;(2)
解析试题分析:(1)根据上表统计得到乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.由于工人乙生产三件产品A,给工厂带来盈利大于或等于100元三种情况是:三件一等品;两件一等品,一件二等品;一件一等品,两件二等品;然后分别计算它们的概率并求和.
(2)由于甲乙分别生产一件产品A给工厂带来的盈利X共有六种情况.分别求的各种情况的概率,根据数学期望公式即可得结论.
试题解析:甲生产一件产品A为一等品、二等品、三等品的概率分别为 , 3分
, 3分
乙生产一件产品A为一等品、二等品、三等品的概率分别为 6分
6分
(1)新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的情形有:三件都是一等品;二件是一等品、一件是二等品或一件是一等品、二件是二等品,概率为: 8分
8分
(2))随机变量X的所有可能取值为100,80,60,40,20,-20.  ,
, ,
, ,
, ,
, ,
,
所以,随机变量 的概率分布为:
的概率分布为:
100 80 60 40 20 -20 






随机变量X的数学期望  (元) 12分
(元) 12分
考点:1.统计概率.2.数学期望的计算.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.样本频率分布表如下:
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
某工厂生产 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
 |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(1)求表格中
 与
与 的值;
的值;(2)从被检测的
 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率. 
 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. 的车辆中任抽取3辆,求抽出的3辆车中车速在
的车辆中任抽取3辆,求抽出的3辆车中车速在 的分布列及数学期望.
的分布列及数学期望.

 本月价格指数
本月价格指数 上月价格指数.规定:当
上月价格指数.规定:当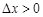 时,称本月价格指数环比增长;
时,称本月价格指数环比增长; 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.

