题目内容
已知一组数据的频率分布直方图如下.求众数、中位数、平均数.
众数为65,中位数为65;平均数为67.
解析试题分析:这是一道从频率分布直方图得到样本数据的数字特征的统计题目,众数是指出现次数最多的数,体现在频率分布直方图中,是指高度最高的小矩形的宽的中点的横坐标,中位数是指从左往右小矩形的面积之和为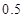 处的横坐标,而平均数则是由各小矩形的宽的中点的横坐标乘以相应小矩形的面积,然后求和得到,故本题按照这些方法进行计算即可得到众数、中位数、平均数的值.
处的横坐标,而平均数则是由各小矩形的宽的中点的横坐标乘以相应小矩形的面积,然后求和得到,故本题按照这些方法进行计算即可得到众数、中位数、平均数的值.
试题解析:由频率分布直方图可知,众数为65,由10×0.03+5×0.04=0.5,所以面积相等的分界线为65,即中位数为65,平均数为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67.
考点:1.频率分布直方图;2.样本数据的数字特征:众数、中位数、平均数.

练习册系列答案
相关题目
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个的概率.
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |

(1)补全频率分布直方图并求n,a,p的值.
(2)为调查该地区的年龄与生活习惯和是否符合低碳观念有无关系,调查组按40岁以下为青年,40岁以上(含40岁)为老年分成两组,请你先完成下面2×2列联表,并回答是否有99%的把握认为该地区的生活习惯是否符合低碳观念与人的年龄有关.
参考公式:χ2=

| P(χ2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |
| 年龄组 是否低碳族 | 青 年 | 老 年 | 总 计 |
| 低碳族 | | | |
| 非低碳族 | | | |
| 总计 | | | |

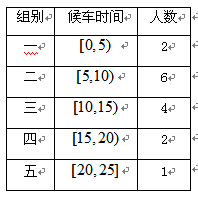

 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
,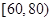 ,
,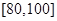 .
.
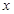 的值;
的值; 分钟的新生,其中2人上学路上时间小于
分钟的新生,其中2人上学路上时间小于 分钟. 从这6人中任选2人,设这2人中上学路上时间小于
分钟. 从这6人中任选2人,设这2人中上学路上时间小于 ,求
,求
 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

 的值;
的值; 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.