题目内容
某班主任对全班50名学生进行了作业量多少的调查.数据如下表:
| | 认为作业多 | 认为作业不多 | 合计 |
| 喜欢玩游戏 | 18 | 9 | |
| 不喜欢玩游戏 | 8 | 15 | |
| 合计 | | | |
(2)试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系?
附:
| P(K2≥K0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

(1)
;(2)说明在犯错误的概率不超过0.025的前提下认为喜欢玩游戏与作业量的多少有关系. 认为作业多 认为作业不多 合计 喜欢玩游戏 18 9 27 不喜欢玩游戏 8 15 23 合计 26 24 50
解析试题分析:(1)根据2×2列联表的知识即可解决;(2)利用公式进行计算,然后与题目所给表格中数据进行比较即可得出结论.
试题解析: (1)
(2)将表中的数据代入公式得到 认为作业多 认为作业不多 合计 喜欢玩游戏 18 9 27 不喜欢玩游戏 8 15 23 合计 26 24 50  的观测值
的观测值
K= ≈5.059>5.024,
≈5.059>5.024,
查表知P(K2≥5.024)=0.025,即说明在犯错误的概率不超过0.025的前提下认为喜欢玩游戏与作业量的多少有关系.
考点:(1)分段函数;(2)频率分布直方图.

练习册系列答案
相关题目
下表是对某市8所中学学生是否吸烟进行调查所得的结果:
| | 吸烟学生 | 不吸烟学生 |
| 父母中至少有一人吸烟 | 816 | 3 203 |
| 父母均不吸烟 | 188 | 1 168 |
(2)在父母均不吸烟的学生中,估计吸烟学生所占的百分比是多少?
(3)学生的吸烟习惯和父母是否吸烟有关吗?请简要说明理由.
(4)有多大的把握认为学生的吸烟习惯和父母是否吸烟有关?
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有一个的概率.
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |

(1)补全频率分布直方图并求n,a,p的值.
(2)为调查该地区的年龄与生活习惯和是否符合低碳观念有无关系,调查组按40岁以下为青年,40岁以上(含40岁)为老年分成两组,请你先完成下面2×2列联表,并回答是否有99%的把握认为该地区的生活习惯是否符合低碳观念与人的年龄有关.
参考公式:χ2=

| P(χ2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |
| 年龄组 是否低碳族 | 青 年 | 老 年 | 总 计 |
| 低碳族 | | | |
| 非低碳族 | | | |
| 总计 | | | |

 本月价格指数
本月价格指数 上月价格指数.规定:当
上月价格指数.规定:当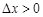 时,称本月价格指数环比增长;
时,称本月价格指数环比增长; 时,称本月价格指数环比下降;当
时,称本月价格指数环比下降;当 时,称本月价格指数环比持平.
时,称本月价格指数环比持平.