题目内容
13.已知钝角α满足$\sqrt{3}sinα-cosα=\frac{8}{5}$,则$tan(α-\frac{π}{6})$=-$\frac{4}{3}$.分析 由两角差的正弦函数公式化简已知等式可得sin(α-$\frac{π}{6}$)=$\frac{4}{5}$,结合角的范围可求cos(α-$\frac{π}{6}$),由同角三角函数关系式即可求得tan(α-$\frac{π}{6}$)的值.
解答 解:∵钝角α满足$\sqrt{3}sinα-cosα=\frac{8}{5}$,
∴$\frac{\sqrt{3}}{2}$sinα-$\frac{1}{2}$cosα=$\frac{4}{5}$,即sin(α-$\frac{π}{6}$)=$\frac{4}{5}$,
∴α-$\frac{π}{6}$≈53°或是127°,
∵α为钝角,前面一种假设显然不成立,
∴α-$\frac{π}{6}$≈127°,
∴cos(α-$\frac{π}{6}$)=-$\frac{3}{5}$,
∴则$tan(α-\frac{π}{6})$=$\frac{sin(α-\frac{π}{6})}{cos(α-\frac{π}{6})}$=-$\frac{4}{3}$.
故答案为:-$\frac{4}{3}$.
点评 本题主要考查了两角差的正弦函数公式,同角三角函数关系式的应用,属于基本知识的考查.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
3.设全集U=R,A={x||x|<2},B={x|y=$\sqrt{x-1}$},则图中阴影部分所表示的集合( )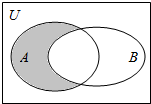

| A. | (-2,+∞) | B. | (1,2] | C. | (-2,1) | D. | (-2,1] |
8.运行如图所示的程序框图,若输出的结果是36,则输入的n=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
2.椭圆C:$\frac{x^2}{16}+\frac{y^2}{9}$=1的左、右顶点分别为A1,A2,点P是C上异于顶点的任一点,则直线PA2与直线PA1的斜率之积是( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{9}{16}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{16}{9}$ |
 过⊙O外一点P作⊙O的切线PA,切点为A,连OP与⊙O交于点C,过C作AP的垂线,垂足为D,若PA=8cm,PC=4cm,则PD的长为3.2.
过⊙O外一点P作⊙O的切线PA,切点为A,连OP与⊙O交于点C,过C作AP的垂线,垂足为D,若PA=8cm,PC=4cm,则PD的长为3.2.