题目内容
18.A、B两仓库分别有编织袋50万个和30万个,由于抗洪抢险的需要,现需调运40万个到甲地,20万个到乙地.已知从A仓库调运到甲、乙两地的运费分别为120元/万个、180元/万个;从B仓库调运到甲、乙两地的运费分别为100元/万个、150元/万个.问如何调运,能使总运费最小?总运费的最小值是多少?分析 设从A仓库调运x万个到甲地,y万个到乙地,总运费记为z元,建立约束条件,利用线性规划进行求解即可.
解答 解:设从A仓库调运x万个到甲地,y万个到乙地,总运费记为z元.
那么需从B仓库调运(40-x)万个到甲地,调运(20-y)万个到乙地.
从而有$\left\{\begin{array}{l}{x+y≤50}\\{40-x+20-y≤30}\\{0≤x≤40}\\{0≤y≤20}\end{array}\right.$,
则z=120x+180y+100(40-x)+150(20-y)=20x+30y+7 000,
作出以上不等式组所表示的平面区域(如图所示),即可行域.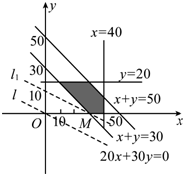
令z′=z-7 000=20x+30y.
作直线l:20x+30y=0,把直线l向右上方平移至l1的位置时,
直线经过可行域上的点M(30,0),且与原点距离最小,
即x=30,y=0时,z=20x+30y取得最小值,
从而z=z′+7 000=20x+30y+7 000亦取得最小值,
zmin=20×30+30×0+7 000=7 600(元).
答:从A仓库调运30万个到甲地,从B仓库调运10万个到甲地,20万个到乙地,可使总运费最小,且总运费的最小值为7 600元.
点评 本题主要考查线性规划的应用问题,根据条件建立约束条件,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
9.某工厂去年的产值为160万元,计划在今后五年内,每一年比上一年产值增加5%,那么从今年起到第五年这个工厂的总产值是( )
| A. | 121.55 | B. | 194.48 | C. | 928.31 | D. | 884.10 |
3.“${log_a}^x={log_a}^y$(a>0且a≠1)”是“x=y”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
10.角α的终边上有一点P(-1,2),则下列结论正确的是( )
| A. | sinα=-$\frac{{2\sqrt{5}}}{5}$ | B. | cosα=-$\frac{{\sqrt{5}}}{5}$ | C. | tanα=-$\frac{1}{2}$ | D. | cosα=$\frac{{\sqrt{5}}}{5}$ |