题目内容
8.若不等式|x+m|+|x-3|<2有解,则m的取值范围是(-5,-1).分析 根据绝对值的意义可得|x+m|+|x-3|最小值为|3+m|,结合后题意可得|3+m|<2,由此求得m的范围.
解答 解:|x+m|+|x-3|表示数轴上的x对应点到-m、3对应点的距离之和,它的最小值为|3+m|,
再结合不等式|x+m|+|x-3|<2有解,可得|3+m|<2,可得-2<m+3<2,
求得-5<m<-1,
故答案为:(-5,-1).
点评 本题主要考查绝对值的意义,绝对值不等式的解法,函数的能成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
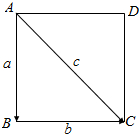 如图所示,已知正方形ABCD的边长等于1,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{AC}$=$\overrightarrow{c}$,试作出下列向量,并分别求出其长度:
如图所示,已知正方形ABCD的边长等于1,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{AC}$=$\overrightarrow{c}$,试作出下列向量,并分别求出其长度: