Question

3．在半径为R的圆形铁皮上割去一个圆心角为θ的扇形，使剩下部分围成一个圆锥，θ为何值时圆锥的容积最大？

Answer 1

分析 在半径为R的圆形铁皮上割去一个圆心角为θ的扇形，设剩下部分的圆周角为α，圆锥的底面半径为r，高为h，体积为V，求出r²+h²=R²，表示出体积表达式，利用导数求出函数的最大值，得到结果．

解答 解：在半径为R的圆形铁皮上割去一个圆心角为θ的扇形，
设剩下部分的圆周角为α，圆锥的底面半径为r，高为h，体积为V，
那么r²+h²=R²，θ=2π-α，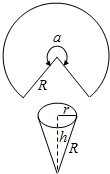

因此，V=$\frac{1}{3}$πr²h
=$\frac{1}{3}$π（R2-h2）h=$\frac{1}{3}$πR2h-$\frac{1}{3}$πh3（0＜h＜R）．…（3分）
V′=$\frac{1}{3}$πR2-πh2．
令V'=0，即$\frac{1}{3}$πR2-πh2=0，得 h=$\frac{\sqrt{3}}{3}$R．…（5分）
当 0＜h＜$\frac{\sqrt{3}}{3}$R时，V'＞0．
当$\frac{\sqrt{3}}{3}$R＜h＜R时，V'＜0．
所以，h=$\frac{\sqrt{3}}{3}$R时，V取得极大值，并且这个极大值是最大值．…（8分）
把 h=$\frac{\sqrt{3}}{3}$R代入r²+h²=R²，得 r=$\frac{\sqrt{6}}{3}$R．
由Rα=2πr，得 α=$\frac{2\sqrt{6}}{3}$π，
则θ=2π-$\frac{2\sqrt{6}}{3}$π，
答：割去一个圆心角为2π-$\frac{2\sqrt{6}}{3}$π弧度时，剩下部分围成圆锥的容积最大．…（12分）

点评 本题考查圆锥与扇形展开图的关系，体积的计算，考查计算能力，导数的应用，解题的关键是建立起体积的函数模型，理解函数的单调性与最值的关系是解本题的重点．