题目内容
13．已知$\overrightarrow{OA}$=（3，1），$\overrightarrow{OB}$=（-1，2），$\overrightarrow{OC}$⊥$\overrightarrow{OB}$，$\overrightarrow{OA}$与$\overrightarrow{BC}$共线，且$\overrightarrow{OA}$+$\overrightarrow{OD}$=$\overrightarrow{OC}$，求$\overrightarrow{OD}$．分析 可设$\overrightarrow{OC}=（a，b）$，$\overrightarrow{OD}=（x，y）$，这样可表示出$\overrightarrow{BC}$=（a+1，b-2），从而根据$\overrightarrow{OC}⊥\overrightarrow{OB}$以及$\overrightarrow{OA}$，$\overrightarrow{BC}$共线即可建立关于a，b的方程组，这样解出a，b，即得出向量$\overrightarrow{OC}$的坐标，再根据$\overrightarrow{OA}+\overrightarrow{OD}=\overrightarrow{OC}$即可求出$\overrightarrow{OD}$的坐标．
解答 解：设$\overrightarrow{OC}=（a，b），\overrightarrow{OD}=（x，y）$；
∵$\overrightarrow{OC}⊥\overrightarrow{OB}$；
∴$\overrightarrow{OC}•\overrightarrow{OB}=0$；
即-a+2b=0 （1）；
$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}$=（a+1，b-2），$\overrightarrow{OA}$与$\overrightarrow{BC}$共线；
∴3（b-2）-（a+1）=0；
即3b-a=7 （2）；
∴（1）（2）联立得a=14，b=7；
$\overrightarrow{OC}=（14，7）$；
又$\overrightarrow{OA}+\overrightarrow{OD}=\overrightarrow{OC}$；
∴（3，1）+（x，y）=（14，7）；
∴$\left\{\begin{array}{l}{3+x=14}\\{1+y=7}\end{array}\right.$；
∴x=11，y=6；
∴$\overrightarrow{OD}=（11，6）$．
点评 考查向量坐标的加法、减法运算，向量数量积的坐标运算，要掌握两向量垂直和平行时的坐标的关系．
| A． | 一定相离 | |
| B． | 一定相切 | |
| C． | 当m＞0时直线与圆相离，当m＜0时直线与圆相交 | |
| D． | 当|m|＜$\sqrt{2}$时直线与圆相离，当|m|＞$\sqrt{2}$时直线与圆相交 |
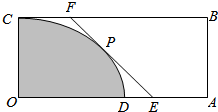如图所示的矩形OABC是某城镇的一块非农业用地，已知图中的点D在边OA上，OC=3km，OD=4km，DA=a km，曲线段CD是分别以OD、OC为长、短半轴的一段椭圆弧．当地政府在新城镇建设中，将图中阴影部分规划为居民区，同时规划过曲线段CD上某一点P修建一条笔直的公路EF，分别与OA、BC交于E、F，且∠OEF=45°．（要求公路不穿越居民区；计算时忽略公路的宽度．）