题目内容
已知函数f(x)=alnx+bx,且f(1)= -1,f′(1)=0,
(1)求f(x);
(2)求f(x)的最大值;
(3)x>0,y>0,证明:lnx+lny≤ .
.
(1)求f(x);
(2)求f(x)的最大值;
(3)x>0,y>0,证明:lnx+lny≤
 .
.(1)f(x)=lnx-x
(2)-1
(3)见解析
(2)-1
(3)见解析
(1)由b=" f(1)=" -1, f′(1)="a+b=0," ∴a=1,∴f(x)=lnx-x为所求;
(2)∵x>0,f′(x)= -1=
-1= ,
,
∴f(x)在x=1处取得极大值-1,即所求最大值为-1;
(3)由(2)得lnx≤x-1恒成立,
∴lnx+lny= +
+ ≤
≤ +
+ =
= 成立
成立
(2)∵x>0,f′(x)=
 -1=
-1= ,
,| x | 0<x<1 | x=1 | x>1 |
| f′(x) | + | 0 | - |
| f(x) | ↗ | 极大值 | ↘ |
∴f(x)在x=1处取得极大值-1,即所求最大值为-1;
(3)由(2)得lnx≤x-1恒成立,
∴lnx+lny=
 +
+ ≤
≤ +
+ =
= 成立
成立
练习册系列答案
相关题目
 ,
, 。
。 在
在 上的值域;
上的值域; ,对
,对 ,
, 恒成立,
恒成立, 的取值范围
的取值范围 ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).

 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围; 的极大值构成的函数
的极大值构成的函数 ,将a换元为x,试判断
,将a换元为x,试判断 是否能与
是否能与 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由.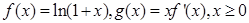 ,其中
,其中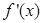 是
是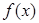 的导函数.
的导函数.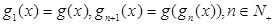 ,
,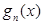 的表达式;
的表达式;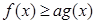 恒成立,求实数
恒成立,求实数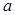 的取值范围;
的取值范围;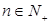 ,比较
,比较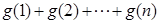 与
与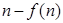 的大小,并加以证明.
的大小,并加以证明. 的部分图像如图所示,则
的部分图像如图所示,则




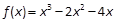 .
.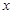 的方程f(x)=a在区间
的方程f(x)=a在区间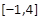 上有三个根,求a的取值范围.
上有三个根,求a的取值范围. 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围;