题目内容
已知函数 ,
, 。
。
(1)求函数 在
在 上的值域;
上的值域;
(2)若 ,对
,对 ,
, 恒成立,
恒成立,
求实数 的取值范围
的取值范围
 ,
, 。
。(1)求函数
 在
在 上的值域;
上的值域;(2)若
 ,对
,对 ,
, 恒成立,
恒成立,求实数
 的取值范围
的取值范围(1)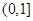 ,(2)
,(2)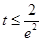 .
.
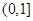 ,(2)
,(2)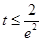 .
.试题分析:(1)利用导数求值域,分四步,第一明确定义域:
 ,第二求导数零点:
,第二求导数零点: 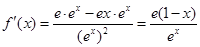 ,令
,令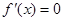 ,得
,得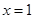 ,第三列表分析单调性:
,第三列表分析单调性: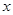 | 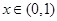 | 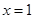 | 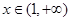 |
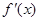 | 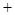 | 0 | — |
 | ↑ | 极大 | ↓ |
第四根据区间端点及极值点确定值域:
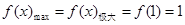 ,又
,又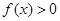 ,所以函数
,所以函数 的值域为
的值域为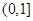 ,(2)恒成立问题,一般转化为最值问题:
,(2)恒成立问题,一般转化为最值问题: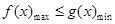 .而
.而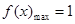 ,
,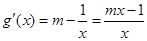 ,由于
,由于 ,故当
,故当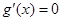 时,
时,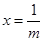 ,所以
,所以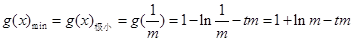 所以
所以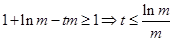 在
在 上恒成立,设
上恒成立,设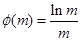 ,
,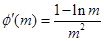 ,令
,令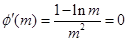 得
得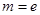 ,又
,又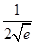 >
>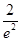 ,所以
,所以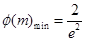 ,所以
,所以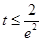 .
.试题解析:(1)
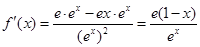 ,令
,令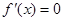 ,得
,得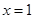 ,
,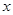 | 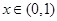 | 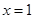 | 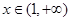 |
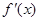 | 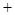 | 0 | — |
 | ↑ | 极大 | ↓ |
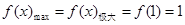 ,又
,又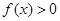 ,所以函数
,所以函数 的值域为
的值域为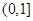 6分
6分(2)依题意
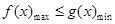 , 8分
, 8分而
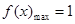 ,
,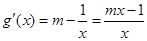 ,由于
,由于 ,故当
,故当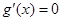 时,
时,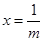 ,
,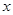 | 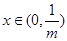 | 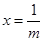 | 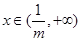 |
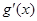 | — | 0 | 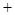 |
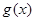 | ↓ | 极小 | ↑ |
所以
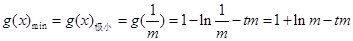 , 10分
, 10分所以
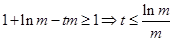 在
在 上恒成立,设
上恒成立,设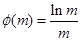 ,
,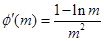 ,令
,令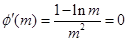 得
得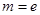 , 12分
, 12分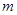 | 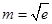 | 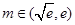 | 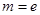 | 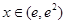 | 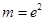 |
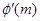 | | 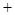 | 0 | — | |
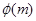 | 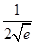 | ↑ | 极大 | ↓ | 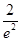 |
又
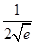 >
>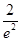 ,所以
,所以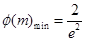 , 14分
, 14分所以
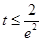 16分
16分
练习册系列答案
相关题目
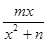 (m,n∈R)在x=1处取得极大值2.
(m,n∈R)在x=1处取得极大值2.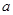 为实数,
为实数,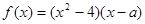
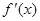 ;
;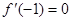 ,求
,求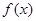 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值. .
.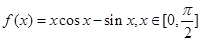 .
. ;
; 对
对 恒成立,求
恒成立,求 的最大值与
的最大值与 的最小值.
的最小值.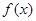 在定义域内可导,
在定义域内可导,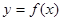 的图象如下右图所示,则导函数
的图象如下右图所示,则导函数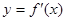 可能为( )
可能为( ) 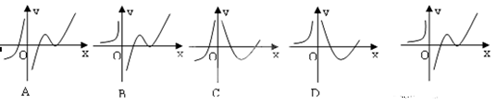
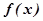 =
=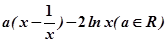 ,
,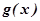 =
=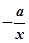 ,若至少存在一个
,若至少存在一个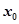 ∈[1,e],使
∈[1,e],使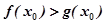 成立,则实数a的范围为( ).
成立,则实数a的范围为( ).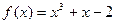 在图象上点P处的切线垂直于直线
在图象上点P处的切线垂直于直线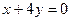 ,则P点的横坐标为( )
,则P点的横坐标为( ) 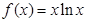 ,若
,若 ,则
,则 ( )
( )


