题目内容
设函数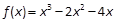 .
.
(1)求f(x)的单调区间和极值;
(2)关于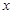 的方程f(x)=a在区间
的方程f(x)=a在区间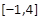 上有三个根,求a的取值范围.
上有三个根,求a的取值范围.
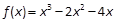 .
.(1)求f(x)的单调区间和极值;
(2)关于
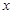 的方程f(x)=a在区间
的方程f(x)=a在区间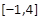 上有三个根,求a的取值范围.
上有三个根,求a的取值范围.(1) f(x)的单调增区间为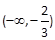 ,
,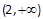 ;单调减区间为
;单调减区间为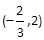 ;当
;当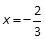 时f(x)有极大值
时f(x)有极大值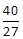 ,当x=2时, f(x)有极小值-8.
,当x=2时, f(x)有极小值-8.
(2)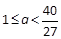
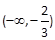 ,
,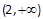 ;单调减区间为
;单调减区间为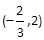 ;当
;当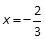 时f(x)有极大值
时f(x)有极大值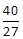 ,当x=2时, f(x)有极小值-8.
,当x=2时, f(x)有极小值-8.(2)
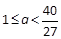
试题分析:(1)首先求出函数的导数,然后根据导数与单调区间的关系确定函数的单调区间,根据函数单调性即可求得函数极值;
(2)关于
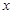 的方程f(x)=a在区间
的方程f(x)=a在区间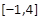 上有三个根,即函数y=a与y=f(x)的图象在区间
上有三个根,即函数y=a与y=f(x)的图象在区间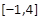 上有三个交点,只需要函数y=" f(x)" 和函数y="a" 的图像有两个交点.根据函数单调性变化情况,可求得实数a的值.
上有三个交点,只需要函数y=" f(x)" 和函数y="a" 的图像有两个交点.根据函数单调性变化情况,可求得实数a的值.(1)
 ,由
,由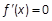 得
得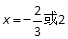 (2分)
(2分)| x | 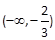 | 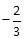 | 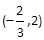 | 2 | 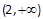 |
| f’(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值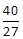 | ↘ | 极小值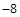 | ↗ |
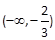 ,
,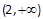 ;单调减区间为
;单调减区间为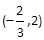 ;
;当
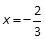 时f(x)有极大值
时f(x)有极大值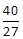 ,当x=2时, f(x)有极小值-8. (6分)
,当x=2时, f(x)有极小值-8. (6分)(2)由题知,只需要函数y=" f(x)" 和函数y="a" 的图像有两个交点. (7分)
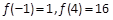 ,所以
,所以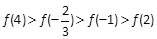
由(1)知f(x)在,当
 上单调递减,
上单调递减, 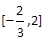 上单调递增,在
上单调递增,在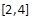 在上单调递减. (10分)
在上单调递减. (10分)∴当
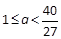 时, y=" f(x)" 和y="a" 的图像有两个交点.即方程f(x)=a在区间
时, y=" f(x)" 和y="a" 的图像有两个交点.即方程f(x)=a在区间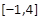 上有三个根. (12分)
上有三个根. (12分)
练习册系列答案
相关题目
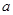 为实数,
为实数,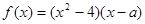
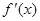 ;
;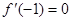 ,求
,求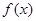 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值.
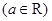 ,已知曲线
,已知曲线 在点
在点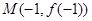 处的切线方程是
处的切线方程是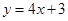 .
. 的值;并求出函数的单调区间;
的值;并求出函数的单调区间; 在区间
在区间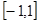 上的最值.
上的最值. .
.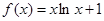
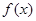 在
在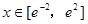 上的最大值与最小值;
上的最大值与最小值;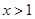 时,函数
时,函数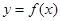 的图像恒在直线
的图像恒在直线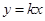 上方,求实数
上方,求实数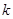 的取值范围;
的取值范围;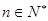 时,
时,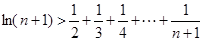
 ,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )
,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )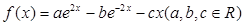 的导函数
的导函数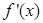 为偶函数,且曲线
为偶函数,且曲线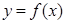 在点
在点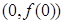 处的切线的斜率为
处的切线的斜率为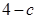 .
.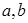 的值;
的值; 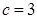 ,判断
,判断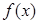 的单调性;
的单调性;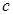 的取值范围.
的取值范围.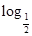 4)f(
4)f(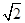 f(
f(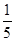 )f(lg
)f(lg