题目内容
设函数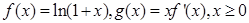 ,其中
,其中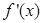 是
是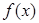 的导函数.
的导函数.
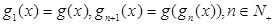 ,
,
(1)求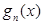 的表达式;
的表达式;
(2)若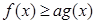 恒成立,求实数
恒成立,求实数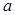 的取值范围;
的取值范围;
(3)设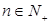 ,比较
,比较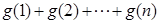 与
与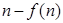 的大小,并加以证明.
的大小,并加以证明.
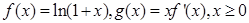 ,其中
,其中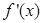 是
是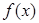 的导函数.
的导函数.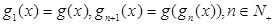 ,
,(1)求
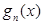 的表达式;
的表达式;(2)若
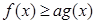 恒成立,求实数
恒成立,求实数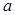 的取值范围;
的取值范围;(3)设
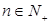 ,比较
,比较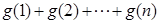 与
与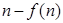 的大小,并加以证明.
的大小,并加以证明.(1)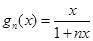 ;(2)
;(2)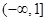 ;(3)
;(3) ,证明见解析.
,证明见解析.
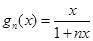 ;(2)
;(2)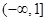 ;(3)
;(3) ,证明见解析.
,证明见解析.试题分析:(1)易得
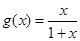 ,且有
,且有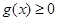 ,当且仅当
,当且仅当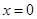 时取等号,当
时取等号,当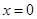 时,
时,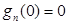 ,当
,当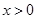 时
时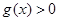 ,由
,由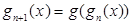 ,得
,得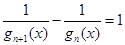 ,所以数列
,所以数列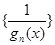 是以
是以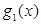 为首项,以1为公差的等差数列,继而得
为首项,以1为公差的等差数列,继而得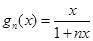 ,经检验
,经检验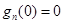 ,所以
,所以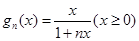 ;
;在
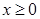 范围内
范围内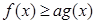 恒成立,等价于
恒成立,等价于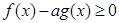 成立,令
成立,令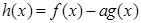
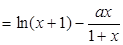 ,即
,即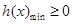 成立,
成立,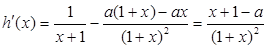 ,令
,令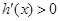 ,得
,得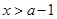 ,分
,分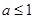 和
和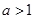 两种情况讨论,分别求出
两种情况讨论,分别求出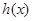 的最小值,继而求出
的最小值,继而求出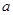 的取值范围;
的取值范围;(3)由题设知:
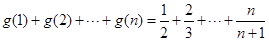 ,
,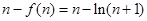 ,比较结果为:
,比较结果为: ,证明如下:上述不等式等价于
,证明如下:上述不等式等价于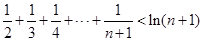
在(2)中取
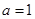 ,可得
,可得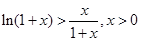 ,令
,令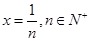 ,则
,则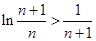 ,即
,即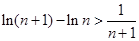 ,使用累加法即可证明结论.
,使用累加法即可证明结论.试题解析:
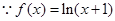 ,
,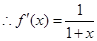 ,
,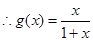
(1)
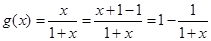
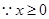 ,
,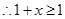 ,
,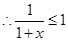 ,
, ,即
,即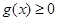 ,当且仅当
,当且仅当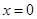 时取等号
时取等号当
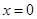 时,
时,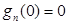
当
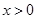 时
时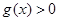
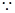
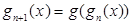
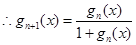 ,
,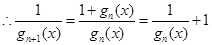 ,即
,即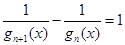
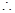 数列
数列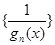 是以
是以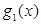 为首项,以1为公差的等差数列
为首项,以1为公差的等差数列
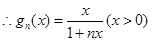
当
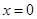 时,
时,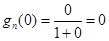
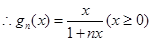
(2)在
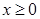 范围内
范围内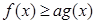 恒成立,等价于
恒成立,等价于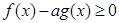 成立
成立令
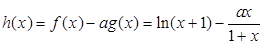 ,即
,即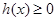 恒成立,
恒成立,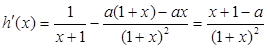
令
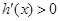 ,即
,即 ,得
,得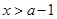
当
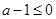 即
即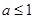 时,
时,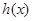 在
在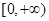 上单调递增
上单调递增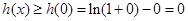
所以当
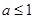 时,
时,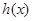 在
在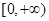 上
上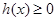 恒成立;
恒成立;当
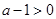 即
即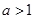 时,
时,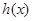 在
在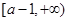 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,所以
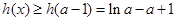
设
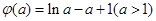
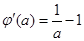
因为
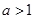 ,所以
,所以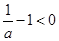 ,即
,即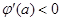 ,所以函数
,所以函数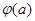 在
在 上单调递减
上单调递减所以
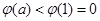 ,即
,即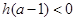
所以
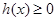 不恒成立
不恒成立综上所述,实数
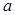 的取值范围为
的取值范围为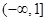
(3)由题设知:
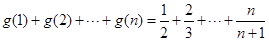 ,
,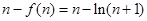
比较结果为:

证明如下:
上述不等式等价于
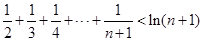
在(2)中取
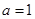 ,可得
,可得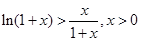
令
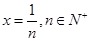 ,则
,则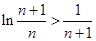 ,即
,即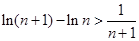
故有
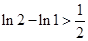
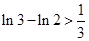
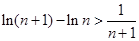
上述各式相加可得:
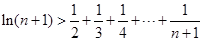
结论得证.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
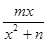 (m,n∈R)在x=1处取得极大值2.
(m,n∈R)在x=1处取得极大值2. .
.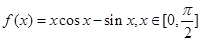 .
. ;
; 对
对 恒成立,求
恒成立,求 的最大值与
的最大值与 的最小值.
的最小值. ,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )
,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )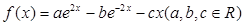 的导函数
的导函数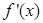 为偶函数,且曲线
为偶函数,且曲线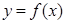 在点
在点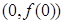 处的切线的斜率为
处的切线的斜率为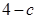 .
.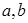 的值;
的值; 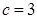 ,判断
,判断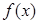 的单调性;
的单调性;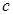 的取值范围.
的取值范围. ,则
,则 等于 ( )
等于 ( ) 处的切线平行于直线
处的切线平行于直线 的坐标是_______.
的坐标是_______.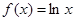 ,则
,则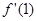 等于( )
等于( )


