题目内容
已知f(x)是定义在集合M上的函数.若区间D⊆M,且对任意x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭.
(1)判断f(x)=x-1在区间[-2,1]上是否封闭,并说明理由;
(2)若函数g(x)= 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围;
(3)若函数h(x)=x3-3x在区间[a,b](a,b∈Z,且a≠b)上封闭,求a,b的值.
(1)判断f(x)=x-1在区间[-2,1]上是否封闭,并说明理由;
(2)若函数g(x)=
 在区间[3,10]上封闭,求实数a的取值范围;
在区间[3,10]上封闭,求实数a的取值范围;(3)若函数h(x)=x3-3x在区间[a,b](a,b∈Z,且a≠b)上封闭,求a,b的值.
(1)函数f(x)在区间[-2,1]上不是封闭的
(2)[3,31]
(3)a=-2,b=2
(2)[3,31]
(3)a=-2,b=2
解:(1)因为函数f(x)=x-1在区间[-2,1]上单调递增,
所以当x∈[-2,1]时,f(x)的值域为[-3,0].
而[-3,0]?[-2,1],所以函数f(x)在区间[-2,1]上不是封闭的.
(2)因为g(x)= =3+
=3+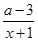 .
.
①当a=3时,函数g(x)=3,显然{3}⊆[3,10],故a=3满足题意;
②当a>3时,在区间[3,10]上,函数g(x)单调递减,此时g(x)的值域为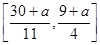 .
.
由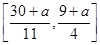 ⊆[3,10]
⊆[3,10]
得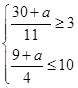 ,解得3≤a≤31,
,解得3≤a≤31,
故3<a≤31;
③当a<3时,在区间[3,10]上,有g(x)=3+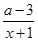 <3,不合题意.
<3,不合题意.
综上所述,实数a的取值范围是[3,31].
(3)因为h(x)=x3-3x,
所以h′(x)=3x2-3=3(x+1)(x-1).
因为当x<-1或x>1时,h′(x)>0;
当x=-1或x=1时,h′(x)=0;
当-1<x<1时,h′(x)<0,
所以函数h(x)在区间(-∞,-1)上单调递增,在区间(-1,1)上单调递减,在区间(1,+∞)上单调递增.
从而h(x)在x=-1处取得极大值2,在x=1处取得极小值-2.
由题意知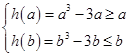
即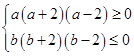
解得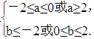
因为a<b,所以-2≤a≤0,0≤b≤2.
又a,b∈Z,故a只可能取-2,-1,0,b只可能取0,1,2.
①当a=-2时,因为b>0,故由h(-1)=2得b≥2,因此b=2.经检验,a=-2,b=2符合题意;
②当a=-1时,由h(-1)=2,得b=2,此时h(1)=-2∉[-1,2],不符合题意;
③当a=0时,显然不符合题意.
综上所述,a=-2,b=2.
所以当x∈[-2,1]时,f(x)的值域为[-3,0].
而[-3,0]?[-2,1],所以函数f(x)在区间[-2,1]上不是封闭的.
(2)因为g(x)=
 =3+
=3+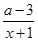 .
.①当a=3时,函数g(x)=3,显然{3}⊆[3,10],故a=3满足题意;
②当a>3时,在区间[3,10]上,函数g(x)单调递减,此时g(x)的值域为
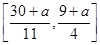 .
.由
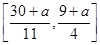 ⊆[3,10]
⊆[3,10]得
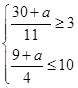 ,解得3≤a≤31,
,解得3≤a≤31,故3<a≤31;
③当a<3时,在区间[3,10]上,有g(x)=3+
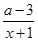 <3,不合题意.
<3,不合题意.综上所述,实数a的取值范围是[3,31].
(3)因为h(x)=x3-3x,
所以h′(x)=3x2-3=3(x+1)(x-1).
因为当x<-1或x>1时,h′(x)>0;
当x=-1或x=1时,h′(x)=0;
当-1<x<1时,h′(x)<0,
所以函数h(x)在区间(-∞,-1)上单调递增,在区间(-1,1)上单调递减,在区间(1,+∞)上单调递增.
从而h(x)在x=-1处取得极大值2,在x=1处取得极小值-2.
由题意知
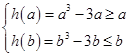
即
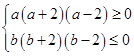
解得
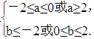
因为a<b,所以-2≤a≤0,0≤b≤2.
又a,b∈Z,故a只可能取-2,-1,0,b只可能取0,1,2.
①当a=-2时,因为b>0,故由h(-1)=2得b≥2,因此b=2.经检验,a=-2,b=2符合题意;
②当a=-1时,由h(-1)=2,得b=2,此时h(1)=-2∉[-1,2],不符合题意;
③当a=0时,显然不符合题意.
综上所述,a=-2,b=2.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 .
.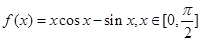 .
. ;
; 对
对 恒成立,求
恒成立,求 的最大值与
的最大值与 的最小值.
的最小值. (
( R),
R),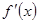 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值 .
.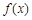 的单调递减区间;
的单调递减区间; ,
, ,当
,当 时,对于任意x,
时,对于任意x, 和
和 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围; (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求
 时,求
时,求 最小值;
最小值; 是单调减函数,求
是单调减函数,求 取值范围.
取值范围.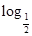 4)f(
4)f(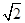 f(
f(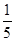 )f(lg
)f(lg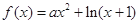 .
.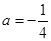 时,求函数
时,求函数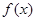 的单调区间;
的单调区间;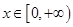 时,函数
时,函数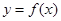 图象上的点都在
图象上的点都在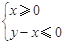 所表示的平面区域内,不等式
所表示的平面区域内,不等式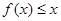 恒成立,求实数
恒成立,求实数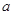 的取值范围.
的取值范围.  ,则
,则 等于 ( )
等于 ( )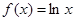 ,则
,则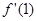 等于( )
等于( )


