题目内容
三次函数f(x)＝mx3－x在(－∞，＋∞)上是减函数，则m的取值范围是 ( )
| A．m<0 | B．m<1 | C．m≤0 | D．m≤1 |
A
f′(x)＝3mx2－1，由题意知，3mx2－1≤0在(－∞，＋∞)上恒成立，则有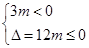
，解得m<0，故选A.
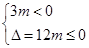，解得m<0，故选A.
练习册系列答案
金钥匙试卷系列答案
相关题目
金钥匙试卷系列答案题目内容
| A．m<0 | B．m<1 | C．m≤0 | D．m≤1 |
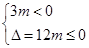，解得m<0，故选A.金钥匙试卷系列答案
(m，n∈R)在x=1处取得极大值2．
为实数，
；
，求
在[－2，2] 上的最大值和最小值.
，已知曲线
在点
处的切线方程是
．
的值；并求出函数的单调区间；
在区间
上的最值．
.
是函数
的一个极值点。⑴求
；⑵求函数
的单调区间；⑶若直线
与函数
的图象有3个交点，求
的取值范围。
，其中s的单位是米，t的单位是秒，那么物体在4秒末的瞬时速度是（ ）
,若
,则
( )
，则
等于 （ ）