题目内容
已知 ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).
(1)
(2)
 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围;
(3)在(2)的条件下,设 的极大值构成的函数
的极大值构成的函数 ,将a换元为x,试判断
,将a换元为x,试判断 是否能与
是否能与 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由.
 ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).(1)

(2)

 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围;(3)在(2)的条件下,设
 的极大值构成的函数
的极大值构成的函数 ,将a换元为x,试判断
,将a换元为x,试判断 是否能与
是否能与 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由.(1) ;(2)使函数
;(2)使函数 在
在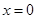 时取得极小值的
时取得极小值的 的取值范围是
的取值范围是 ;(3)不能相切,过程见解析.
;(3)不能相切,过程见解析.
 ;(2)使函数
;(2)使函数 在
在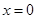 时取得极小值的
时取得极小值的 的取值范围是
的取值范围是 ;(3)不能相切,过程见解析.
;(3)不能相切,过程见解析.试题分析:(1)当
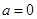 时,
时, ,先求导函数
,先求导函数 ,将
,将 代入可得
代入可得 ;(2)
;(2) ,令
,令 ,得
,得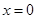 或
或 ,对
,对 进行讨论,当
进行讨论,当 时,
时, 在区间
在区间 上单调递减,没有极小值,当
上单调递减,没有极小值,当 时,
时,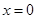 是函数
是函数 的极小值点,当
的极小值点,当 时,
时,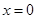 是函数
是函数 的极大值点;(3)极大值为
的极大值点;(3)极大值为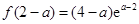 ,则
,则 ,可得
,可得 ,令
,令 则
则 恒成立,即
恒成立,即 在区间
在区间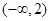 上是增函数.当
上是增函数.当 时,
时, ,即恒有
,即恒有 ,直线斜率为
,直线斜率为 ,不可能相切.
,不可能相切.解(1)当
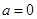 时,
时, .
. .
.所以
 .
.(2)

 .
.令
 ,得
,得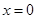 或
或 .
.当
 ,即
,即 时,
时, 恒成立,
恒成立,此时
 在区间
在区间 上单调递减,没有极小值;
上单调递减,没有极小值;当
 ,即
,即 时,
时, 若
 ,则
,则 .若
.若 ,则
,则 .
.所以
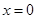 是函数
是函数 的极小值点.
的极小值点.当
 ,即
,即 时,
时,若
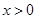 ,则
,则 .若
.若 ,则
,则 .
.此时
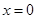 是函数
是函数 的极大值点.
的极大值点.综上所述,使函数
 在
在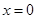 时取得极小值的
时取得极小值的 的取值范围是
的取值范围是 .
.(3)由(2)知当
 ,且
,且 时,
时, ,
,因此
 是
是 的极大值点,极大值为
的极大值点,极大值为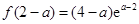 .
.所以
 .
. .
.令
 .
.则
 恒成立,即
恒成立,即 在区间
在区间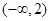 上是增函数.
上是增函数.所以当
 时,
时, ,即恒有
,即恒有 .
.又直线
 的斜率为
的斜率为 ,
,所以曲线
 不能与直线
不能与直线 相切.
相切.
练习册系列答案
相关题目
 .
.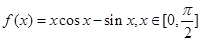 .
. ;
; 对
对 恒成立,求
恒成立,求 的最大值与
的最大值与 的最小值.
的最小值. (
( R),
R),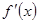 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值 .
.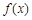 的单调递减区间;
的单调递减区间; ,
, ,当
,当 时,对于任意x,
时,对于任意x, 和
和 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围; (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求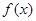 在定义域内可导,
在定义域内可导,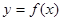 的图象如下右图所示,则导函数
的图象如下右图所示,则导函数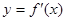 可能为( )
可能为( ) 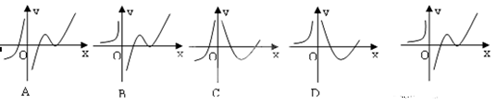
 ,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )
,其中s的单位是米,t的单位是秒,那么物体在4秒末的瞬时速度是( )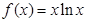 ,若
,若 ,则
,则 ( )
( )



 ,则
,则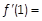 ( ).
( ).



 处的切线平行于直线
处的切线平行于直线 的坐标是_______.
的坐标是_______.