题目内容
20.(本小题满分14分)
已知抛物线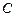 :
: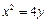 的焦点为
的焦点为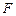 ,过点
,过点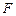 作直线
作直线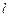 交抛物线
交抛物线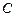 于
于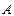 、
、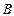 两点;椭圆
两点;椭圆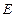 的中心在原点,焦点在
的中心在原点,焦点在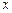 轴上,点
轴上,点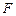 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率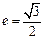 .
.
(1)求椭圆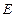 的方程;
的方程;
(2)经过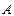 、
、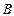 两点分别作抛物线
两点分别作抛物线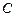 的切线
的切线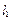 、
、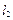 ,切线
,切线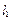 与
与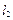 相交于点
相交于点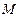 .证明:
.证明: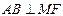 ;
;
(3)椭圆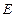 上是否存在一点
上是否存在一点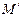 ,经过点
,经过点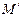 作抛物线
作抛物线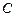 的两条切线
的两条切线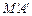 、
、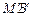 (
(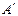 、
、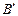 为切点),使得直线
为切点),使得直线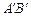 过点
过点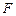 ?若存在,求出抛物线
?若存在,求出抛物线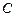 与切线
与切线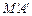 、
、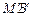 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由.
已知抛物线
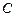 :
: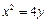 的焦点为
的焦点为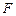 ,过点
,过点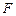 作直线
作直线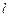 交抛物线
交抛物线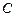 于
于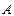 、
、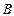 两点;椭圆
两点;椭圆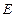 的中心在原点,焦点在
的中心在原点,焦点在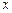 轴上,点
轴上,点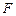 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率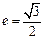 .
.(1)求椭圆
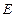 的方程;
的方程;(2)经过
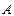 、
、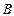 两点分别作抛物线
两点分别作抛物线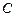 的切线
的切线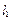 、
、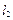 ,切线
,切线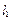 与
与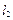 相交于点
相交于点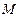 .证明:
.证明: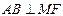 ;
;(3)椭圆
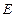 上是否存在一点
上是否存在一点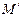 ,经过点
,经过点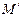 作抛物线
作抛物线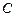 的两条切线
的两条切线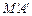 、
、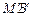 (
(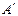 、
、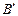 为切点),使得直线
为切点),使得直线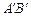 过点
过点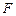 ?若存在,求出抛物线
?若存在,求出抛物线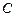 与切线
与切线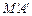 、
、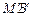 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由. |
 ,
,
 20.(本小题满分14分)
20.(本小题满分14分)(考查椭圆、抛物线、直线、定积分等知识,考查数形结合、化归转化等数学思想、以及推理论证能力和运算求解能力)
解:(1)设椭圆
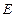 的方程为
的方程为 ,半焦距为
,半焦距为 .
.由已知条件,得
 ,
,∴

解得
 .
.所以椭圆
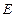 的方程为:
的方程为: . …………
. ………… 分
分(2)显然直线
 的斜率存在,否则直线
的斜率存在,否则直线 与抛物线
与抛物线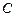 只有一个交点,不合题意,
只有一个交点,不合题意,故可设直线
 的方程为
的方程为  ,
, ,
,由

消去
 并整理得
并整理得 ,
,∴
 . …………
. ………… 分
分∵抛物线
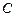 的方程为
的方程为 ,求导得
,求导得 ,
,∴过抛物线
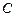 上
上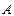 、
、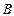 两点的切线方程分别是
两点的切线方程分别是 ,
,  ,
,即
 ,
,  ,
,解得两条切线
 、
、 的交点
的交点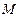 的坐标为
的坐标为 ,即
,即 ,……
,…… 分
分∴



∴
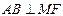 . …………
. ………… 分
分(3)假设存在点
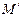 满足题意,由(2)知点
满足题意,由(2)知点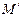 必在直线
必在直线 上,又直线
上,又直线 与椭圆
与椭圆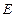 有唯一交点,故
有唯一交点,故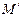 的坐标为
的坐标为 ,
, 设过点
设过点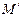 且与抛物线
且与抛物线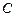 相切的切线方程为:
相切的切线方程为: ,其中点
,其中点 为切点.
为切点.令
 得,
得, ,
,解得
 或
或 , …………
, ………… 分
分故不妨取
 ,即直线
,即直线 过点
过点 .
.综上所述,椭圆
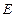 上存在一点
上存在一点 ,经过点
,经过点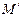 作抛物线
作抛物线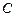 的两条切线
的两条切线 、
、 (
(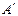 、
、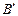 为切点),能使直线
为切点),能使直线 过点
过点 .
.此时,两切线的方程分别为
 和
和 . …………
. ………… 分
分抛物线
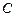 与切线
与切线 、
、 所围成图形的面积为
所围成图形的面积为 .
. 
练习册系列答案
相关题目
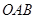 的三个顶点都在抛物线
的三个顶点都在抛物线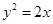 上,其中
上,其中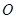 为坐标原点,设圆
为坐标原点,设圆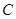 是
是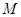 的方程为
的方程为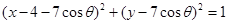 ,过圆
,过圆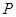 分别作圆
分别作圆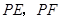 ,切点为
,切点为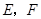 ,求
,求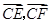 的最大值和最小值.
的最大值和最小值.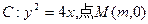 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线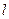 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。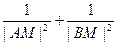 恒为定值。
恒为定值。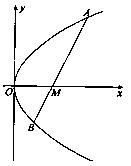
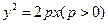 的焦点与椭圆
的焦点与椭圆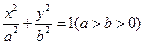 的一个焦点重合,且抛物线与椭圆的一个交点为
的一个焦点重合,且抛物线与椭圆的一个交点为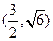 ,(1)求抛物线与椭圆的方程,(2)若过点
,(1)求抛物线与椭圆的方程,(2)若过点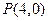 的直线与抛物线交于点
的直线与抛物线交于点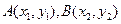 ,求
,求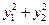 的最小值
的最小值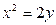 上距
上距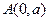 (
(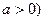 最近的点恰好是顶点的充要条件是什么
最近的点恰好是顶点的充要条件是什么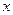 轴上,且经过点
轴上,且经过点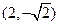 的抛物线的方程为( )
的抛物线的方程为( )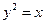
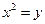
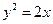
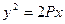 的一条焦点弦AB被焦点F分成长为m、n的两部分,求证:
的一条焦点弦AB被焦点F分成长为m、n的两部分,求证: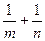 为定值
为定值 如图,F是抛物线
如图,F是抛物线 的焦点,Q为准线与
的焦点,Q为准线与 轴的交点,直线
轴的交点,直线 经过点Q.
经过点Q. ,
, .求证:
.求证: 为定值.
为定值.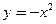 的焦点坐标为( )
的焦点坐标为( ) )
) )
)