Question

【题目】已知函数f (x)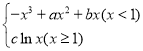＝的图象在点(－2，f (－2))处的切线方程为16x＋y＋20＝0.

（1）求实数a、b的值；

（2）求函数f(x)在区间[－1，2]上的最大值；

Answer 1

【答案】(1);(2)当时,在上的最大值为；当时, 在上的最大值为.

【解析】

(1)利用函数图象在点处的切线方程为,结合导数的几何意义列出关于的关系式再求解即可.
(2)根据分段函数,分类讨论的范围,利用函数的单调性,即可求在上的最大值；

(1)当时,,因为函数图象在点处的切线方程为,所以切点坐标为，

所以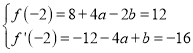,解得；

(2)由(1)得,当时,,

令可得或,故函数在和上单调递减,在上单调递增.

∴时,的最大值为；

当时,.

当时,恒成立, ,此时在上的最大值为；

当时,在上单调递增,且

令,则,

∴当时,在上的最大值为；

当时, 在上的最大值为

综上,当时, 在上的最大值为,当时, 在上的最大值为.