题目内容
【题目】将一颗质地均匀的正方体骰子（六个面的点数分别为1、2、3、4、5、6）先后抛掷两次，记第一次出现的点数为
，第二次出现的点数为
.
（1）设复数
（
为虚数单位），求事件“
为实数”的概率；
（2）求点
落在不等式组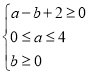
表示的平面区域内（含边界）的概率.
【答案】（1）
（2）
【解析】
（1）根据
为实数求得
，求出符合条件的
的个数，用概率的计算公式求解即可；
（2）先求出抛掷两次骰子的基本事件总数，画出平面区域，再求出满足条件的基本事件数，即可求得概率.
（1）
（
为虚数单位），为实数，
则
为实数，所以.
依题意得的可能取值为1、2、3、4、5、6，
故的概率为.
即事件“为实数”的概率为.
（2）连续抛掷两次骰子所得结果如下表：
1 | 2 | 3 | 4 | 5 | 6 | |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
由上表知，连续抛掷两次骰子共有36种不同的结果.
不等式组所表示的平面区域如图中阴影部分所示（含边界）.
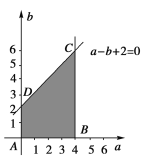
由图知 点
落在四边形
内的结果有：
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
，共18种.
所以点落在四边形内（含边界）的概率
.
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
