题目内容
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,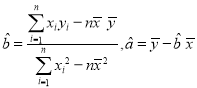 .
.
【答案】(1)![]() ,预计到2022年该公司的网购人数能超过300万人;
,预计到2022年该公司的网购人数能超过300万人;
(2)约400元.
【解析】
(1)依题意,先求出![]() ,代入公式即可得到
,代入公式即可得到![]() ,
,![]() ,可得回归方程为
,可得回归方程为![]() ,令
,令![]() ,
,![]() .所以预计到2022年该公司的网购人数能超过300万;
.所以预计到2022年该公司的网购人数能超过300万;
(2)遥控车移到第![]() (
(![]() )格的情况是下列两种,而且也只有两种.
)格的情况是下列两种,而且也只有两种.
①遥控车先到第![]() 格,又掷出偶数,其概率为
格,又掷出偶数,其概率为![]()
②遥控车先到第![]() 格,又掷出奇数,其概率为
格,又掷出奇数,其概率为![]()
所以![]() ,即可证得
,即可证得![]() 是等比数列,
是等比数列,
利用累加法求出数列![]() 的通项公式,即可求得失败和获胜的概率,从而计算出期望.
的通项公式,即可求得失败和获胜的概率,从而计算出期望.
解:(1)![]()
![]()
![]()
![]()
故![]() 从而
从而![]()
所以所求线性回归方程为![]() ,
,
令![]() ,解得
,解得![]() .
.
故预计到2022年该公司的网购人数能超过300万人
(2)遥控车开始在第0格为必然事件,![]() ,第一次掷骰子出现奇数,遥控车移到第一格,其概率为
,第一次掷骰子出现奇数,遥控车移到第一格,其概率为![]() ,即
,即![]() .遥控车移到第
.遥控车移到第![]() (
(![]() )格的情况是下列两种,而且也只有两种.
)格的情况是下列两种,而且也只有两种.
①遥控车先到第![]() 格,又掷出奇数,其概率为
格,又掷出奇数,其概率为![]()
②遥控车先到第![]() 格,又掷出偶数,其概率为
格,又掷出偶数,其概率为![]()
所以![]() ,
,![]()
![]() 当
当![]() 时,数列
时,数列![]() 是公比为
是公比为![]() 的等比数列
的等比数列
![]()
以上各式相加,得![]()
![]()
![]() (
(![]() ),
),
![]() 获胜的概率
获胜的概率![]()
失败的概率![]()
![]() 设参与游戏一次的顾客获得优惠券金额为
设参与游戏一次的顾客获得优惠券金额为![]() 元,
元,![]() 或
或![]()
![]() X的期望
X的期望![]()
![]() 参与游戏一次的顾客获得优惠券金额的期望值为
参与游戏一次的顾客获得优惠券金额的期望值为![]() ,约400元.
,约400元.

【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市12月1日-20日AQI指数变化趋势:

下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占![]()
C.该市12月的前半个月的空气质量越来越好
D.总体来说,该市12月上旬的空气质量比中旬的空气质量好