题目内容
【题目】如图所示,在四棱台![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 为菱形,
为菱形,![]() ,
,![]() .
.
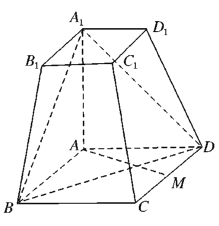
(1)若![]() 为
为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题(1)连接![]() ,可证
,可证![]() ,又因为
,又因为![]() 底面
底面![]() ,可得
,可得![]() ,即可得证.
,即可得证.
(2)如图建立空间直角坐标系![]() ,求出
,求出![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() 的坐标,则直线
的坐标,则直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.
试题解析:
(Ⅰ)∵四边形![]() 为菱形,
为菱形,![]() ,连结
,连结![]() ,则
,则![]() 为等边三角形,
为等边三角形,
又∵![]() 为
为![]() 中点∴
中点∴![]() ,由
,由![]() 得∴
得∴![]()
∵![]() 底面
底面![]() ,
,![]() 底面
底面![]() ∴
∴![]() ,又∵
,又∵![]()
∴![]() 平面
平面![]()
(Ⅱ)∵四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,
,
得![]() ,
,![]() ,∴
,∴![]() 又∵
又∵![]() 底面
底面![]() ,
,
分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]()
![]() 、
、![]() 、
、![]() 、
、![]()
∴![]() ,
,![]() ,
,![]()
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则有 ,令
,令![]() ,则
,则![]()
∴直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值
的正弦值
 .
.

点晴:本题考查的空间的线面关系以及空间的角.第一问通过证明直线![]() 和平面
和平面![]() 内的两条相交直线
内的两条相交直线![]() 垂直,证明
垂直,证明![]() 平面
平面![]() ;第二问中通过建立空间直角坐标系
;第二问中通过建立空间直角坐标系![]() ,求得
,求得![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]()
,结合![]() 得到结论.
得到结论.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
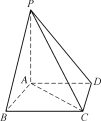
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的650名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: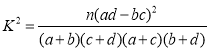 ,其中
,其中![]() .
.
