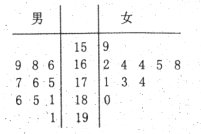
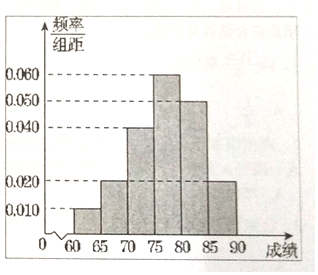
题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若存在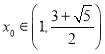 ,使函数
,使函数![]() 的图像在点
的图像在点![]() 和点
和点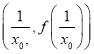 处的切线互相垂直,求
处的切线互相垂直,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 在区间
在区间![]() 上有两个极值点,则是否存在实数
上有两个极值点,则是否存在实数![]() ,使
,使![]() 对任意的
对任意的![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
试题分析:(1)借助题设条件建立方程求解;(2)借助题设依据导数知识建立函数求解;(3)借助题设条件运用二次函数的知识建立不等式组探求.
试题解析:
(1)由![]() 得,
得,
![]() ,解得
,解得![]()
(2)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,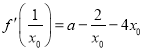 ,
,
由题意得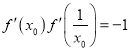 ,即
,即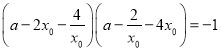 ,
,
整理得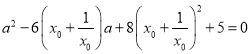 ,
,
设![]() ,由
,由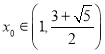 ,得
,得![]() ,
,
则有![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上有零点,
上有零点,
考虑到![]() ,
,
所以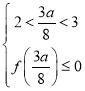 或
或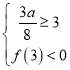 ,解得
,解得![]() 或
或![]() ,
,
所以![]() 的取值范围是
的取值范围是![]()
(3)![]() ,
,
令![]() ,由题意,
,由题意,![]() 在区间
在区间![]() 上有两个不同零点,
上有两个不同零点,
则有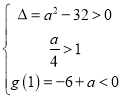 ,解得
,解得![]()
设函数![]() 的两个极值点为
的两个极值点为![]() 和
和![]() ,
,
则![]() 和
和![]() 是
是![]() 在区间
在区间![]() 上的两个不同零点,
上的两个不同零点,
不妨设![]() ,则
,则![]() ①,
①,
得![]() 且关于
且关于![]() 在
在![]() 上递增,
上递增,
因此![]()
又由①可得![]() ②,
②,
当![]() 时,
时,![]() 递减;
递减;
![]() 时,
时,![]() 递增;
递增;
当![]() 时,
时,![]() 递减,
递减,
结合②可得![]()
![]()
设![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上递增,
上递增,
所以![]() ,从而
,从而![]() ,
,
所以![]() ,
,
又![]() ,所以存在
,所以存在![]() ,使
,使![]() ,
,
综上,存在满足条件的![]() ,
,![]() 的取值范围为
的取值范围为![]()

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年利润
(单位:千元)对年利润![]() (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费![]() 和年利润
和年利润![]() (
(![]() )进行了统计,列出了下表:
)进行了统计,列出了下表:
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合![]() 与
与![]() 的关系,请你帮助建立
的关系,请你帮助建立![]() 关于
关于![]() 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)
(2)小李决定选择对数回归模型拟合![]() 与
与![]() 的关系,得到了回归方程:
的关系,得到了回归方程:![]() ,并提供了相关指数
,并提供了相关指数![]() .请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析分析数据
.请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析分析数据![]() )
)
参考公式:相关指数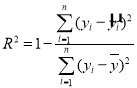
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]() .
.