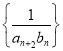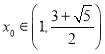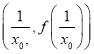题目内容
【题目】设等差数列![]() 是无穷数列,且各项均为互不相同的正整数,其前
是无穷数列,且各项均为互不相同的正整数,其前![]() 项和为
项和为![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若数列![]() 为等差数列,求
为等差数列,求![]() ;
;
(3)在(1)的条件下,求证:数列![]() 中存在无穷多项(按原来的顺序)成等比数列.
中存在无穷多项(按原来的顺序)成等比数列.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)由![]() 列方程组求得
列方程组求得![]() 与
与![]() ,进而可得结果;(2)由
,进而可得结果;(2)由![]() 为等差数列可得
为等差数列可得![]() 结合
结合![]() 可得
可得![]() 从而可得结果;(3)由
从而可得结果;(3)由![]() 可得对任意的
可得对任意的![]() ,
, ![]() 都是
都是![]() 中的项.
中的项.
试题解析:(1)设等差数列![]() 的公差为
的公差为![]() ,
,
因为无穷数列![]() 的各项均为互不相同的正整数,所以
的各项均为互不相同的正整数,所以![]() ,
,
(1)由![]() 得,
得, ![]() ,
,
解得![]() ,所以
,所以![]() ;
;
(2)因为数列![]() 为等差数列,所以
为等差数列,所以![]() ,即
,即 ,
,
所以![]() ,解得
,解得![]() (
(![]() 已舍),
已舍),
此时,  ;
;
(3)由(1)知,等差数列![]() 的通项公式
的通项公式![]() ,
,
下证:对任意的![]() ,
, ![]() 都是
都是![]() 中的项,
中的项,
证明:当![]() 时,因为
时,因为![]() ,
,
所以![]()
![]() ,其中
,其中![]() ,
,
又![]() 时,
时, ![]() ,
,
所以对任意的![]() ,
, ![]() 都是
都是![]() 中的项,
中的项,
所以,数列![]() 中存在无穷项(按原来的顺序)成等比数列.
中存在无穷项(按原来的顺序)成等比数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数比女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(Ⅰ)根据题意建立的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(Ⅱ)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
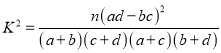 ,
, ![]() .
.