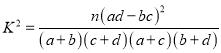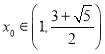题目内容
【题目】若对于定义在![]() 上的连续函数
上的连续函数![]() ,存在常数
,存在常数![]() (
(![]() ),使得
),使得![]() 对任意的实数
对任意的实数![]() 成立,则称
成立,则称![]() 是回旋函数,且阶数为
是回旋函数,且阶数为![]() .
.
(1)试判断函数![]() 是否是一个阶数为1的回旋函数,并说明理由;
是否是一个阶数为1的回旋函数,并说明理由;
(2)已知![]() 是回旋函数,求实数
是回旋函数,求实数![]() 的值;
的值;
(3)若回旋函数![]() (
(![]() )在
)在![]() 恰有100个零点,求实数
恰有100个零点,求实数![]() 的值.
的值.
【答案】(1)![]() 是一个阶数为1的回旋函数;(2)
是一个阶数为1的回旋函数;(2)![]() ,
, ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据“回旋函数”、“阶数”的定义,只需证明![]() 即可;(2)
即可;(2)![]() 是
是![]() 阶回旋函数,则
阶回旋函数,则![]() 恒成立,由三角函数的值域可知
恒成立,由三角函数的值域可知![]() ,然后解简单的三角方程即可得结果;(3)根据“回旋函数”的定义可得,
,然后解简单的三角方程即可得结果;(3)根据“回旋函数”的定义可得, ![]() ,根据正弦函数的周期性结合图象即可得结果.
,根据正弦函数的周期性结合图象即可得结果.
试题解析:(1)![]()
![]() ,
,
![]() 函数
函数![]() 是一个阶数为1的回旋函数.
是一个阶数为1的回旋函数.
(2)设![]() 是
是![]() 阶回旋函数,则
阶回旋函数,则![]() ,
,
若![]() ,上式对任意实数
,上式对任意实数![]() 均成立;
均成立;
若![]() ,
, ![]() ,由三角函数的值域可知
,由三角函数的值域可知![]() ,
,
当![]() 时,对任意实数
时,对任意实数![]() 有
有![]() ;
;
则![]() ,
, ![]() ,所以
,所以![]() .
.
当![]() 时,对任意实数
时,对任意实数![]() 有
有![]() ;
;
则![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() .
.
综上所述: ![]() ,
, ![]() .
.
(3)![]()
![]() ,对任意的
,对任意的![]() 都成立.
都成立.
由(2)可知![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
令![]() ,解得
,解得![]() (
(![]() ).
).
![]() 函数
函数![]() 在
在![]() 恰有100个零点,
恰有100个零点, ![]() ,
,
![]() .又
.又![]() ,
, ![]() ,
,
![]() .
.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】某种产品的年销售量![]() 与该年广告费用支出
与该年广告费用支出![]() 有关,现收集了4组观测数据列于下表:
有关,现收集了4组观测数据列于下表:
| 1 | 4 | 5 | 6 |
| 30 | 40 | 60 | 50 |
现确定以广告费用支出![]() 为解释变量,销售量
为解释变量,销售量![]() 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.
(1)已知这两个变量满足线性相关关系,试建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(2)假如2017年广告费用支出为10万元,请根据你得到的模型,预测该年的销售量![]() .
.
(线性回归方程系数公式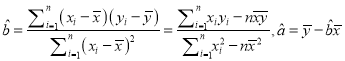 ).
).
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |