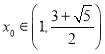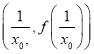题目内容
【题目】数列
满足
， 
.
（1）证明：数列
是等差数列；
（2）设
，数列
的前
项和为
，对任意的
， 
， 
恒成立，求正数
的取值范围.
【答案】（1）证明见解析 （2）
【解析】试题分析：（1）根据等差数列的定义即可证明：数列
是等差数列；
（2）利用错位相减法即可求数列{bn}的前n项和
，利用作差法可得数列{
}单调递增， 
， 
恒成立，只需
即可.
试题解析：
解（1）证明：由已知可得
＝
，
即
＝
＋1，即－＝1.
∴数列
是公差为1的等差数列．
（2）由(1)知＝
＋(n－1)×1＝n＋1，
∴an＝
.
所以bn＝
，
Tn＝
＋
＋
＋…＋，
Tn＝
＋
＋
＋…＋
.
两式相减得
Tn＝＋2
－，
Tn＝＋2×
－，
Tn＝1＋4
－＝3－
，
由Tn－Tn－1＝3－－
＝，
当n≥2时，Tn－Tn－1>0，所以数列{Tn}单调递增．
最小为
，
依题意
上恒成立，
设
则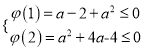
又
解得
练习册系列答案
相关题目
【题目】某单位需要从甲、乙
人中选拔一人参加新岗位培训，特别组织了
个专项的考试，成绩统计如下：
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
（1）根据有关统计知识，回答问题:若从甲、乙
人中选出
人参加新岗培训，你认为选谁合适，请说明理由；
（2）根据有关槪率知识，解答以下问题：
从甲、乙
人的成绩中各随机抽取一个，设抽到甲的成绩为
，抽到乙的成绩为
，用
表示满足条件
的事件，求事件
的概率.