题目内容
【题目】如图，三棱台
的底面是正三角形，平面
平面
，
，
.
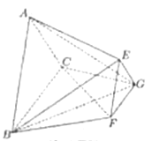
（Ⅰ）求证：
；
（Ⅱ）若
和梯形的面积都等于
，求三棱锥
的体积.
【答案】（I）见证明；（II）
【解析】
（Ⅰ）取
的中点为
，连结
，可证明四边形
为平行四边形，得
，由等腰三角形的性质得
，可得
，由面面垂直的性质可得
平面
，从而可得结果；（Ⅱ）由三棱台
的底面是正三角形，且
，可得
，由此
，
.根据面积相等求得棱锥的高，利用棱锥的体积公式可得结果.
（Ⅰ）取的中点为，连结.
由是三棱台得，平面
平面
，∴
.
∵，
∴
，
∴四边形为平行四边形，∴.
∵
，为的中点，
∴，∴.
∵平面
平面
，且交线为，
平面，
∴平面，而
平面，
∴
.
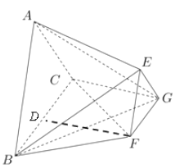
（Ⅱ）∵三棱台的底面是正三角形，且，
∴，∴，
∴.
由（Ⅰ）知，平面.
∵正
的面积等于
，∴
，
.
∵直角梯形的面积等于，
∴
，∴
，
∴
.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】为保护农民种粮收益，促进粮食生产，确保国家粮食安全，调动广大农民粮食生产的积极性，从2004年开始，国家实施了对种粮农民直接补贴.通过对2014～2018年的数据进行调查，发现某地区发放粮食补贴额
（亿元）与该地区粮食产量
（万亿吨）之间存在着线性相关关系.统计数据如下表：
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
补贴额 | 9 | 10 | 12 | 11 | 8 |
粮食产量 | 23 | 25 | 30 | 26 | 21 |
（1）请根据如表所给的数据，求出关于的线性回归直线方程
；
（2）通过对该地区粮食产量的分析研究，计划2019年在该地区发放粮食补贴额7亿元，请根据（1）中所得的线性回归直线方程，预测2019年该地区的粮食产量.
（参考公式：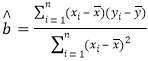
，
）
