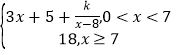题目内容
【题目】已知直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 并与圆C相切的直线方程.
并与圆C相切的直线方程.
【答案】(1)1;(2) ![]() 或
或![]() .
.
【解析】
(1)求出圆心到直线的距离,由勾股定理列出关于![]() 的方程,解之可得;
的方程,解之可得;
(2)点在圆外,因此考虑斜率不存在的情形是否满足题意,在斜率存在时,设斜率为![]() ,写出切线方程,由圆心到切线的距离等于半径求得
,写出切线方程,由圆心到切线的距离等于半径求得![]() .
.
(1)依题意可得圆心C(a,2),半径r=2,
则圆心到直线l:x﹣y+3=0的距离 ,
,
由勾股定理可知![]() ,代入化简得|a+1|=2,
,代入化简得|a+1|=2,
解得a=1或a=﹣3,又a>0,
所以a=1;
(2)由(1)知圆C:(x﹣1)2+(y﹣2)2=4,又(3,5)在圆外,
∴①当切线方程的斜率存在时,设方程为y﹣5=k(x﹣3),由圆心到切线的距离d=r=2可解得![]() ,
,
∴切线方程为5x﹣12y+45=0,
②当过(3,5)斜率不存在,易知直线x=3与圆相切,
综合①②可知切线方程为5x﹣12y+45=0或x=3.

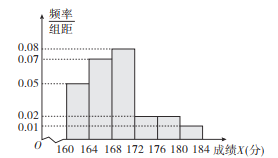
【题目】某企业三月中旬生产![]() ,
,![]() ,
,![]() 三种产品共3000件,根据分层随机抽样的结果,企业统计员制作了如下的统计表格:
三种产品共3000件,根据分层随机抽样的结果,企业统计员制作了如下的统计表格:
产品类别 |
|
|
|
产品数量 | 1300 | ||
样本中的数量 | 130 |
由于不小心,表格中![]() ,
,![]() 产品的有关数据已被污染得看不清楚,统计员只记得样本中
产品的有关数据已被污染得看不清楚,统计员只记得样本中![]() 产品的数量比样本中
产品的数量比样本中![]() 产品的数量多10.根据以上信息,求该企业生产
产品的数量多10.根据以上信息,求该企业生产![]() 产品的数量.
产品的数量.
【题目】某教育部门为了了解某地区高中学生每周的课外羽毛球训练的情况,随机抽取了该地区50名学生进行调查,其中男生25人.将每周课外训练时间不低于8小时的学生称为“训练迷”,低于8小时的学生称为“非训练迷”.已知“训练迷”中有15名男生.根据调查结果绘制的学生每周课外训练时间的频率分布直方图(时间单位为小时)如图所示.
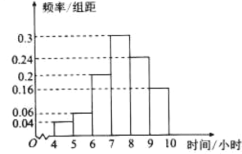
(1)根据图中数据估计该地区高中学生每周课外训练的平均时间(说明:同一组中的数据用该组区间的中间值作代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
列联表,并判断是否有99.5%的把握认为“训练迷”与性别有关?
非训练迷 | 训练迷 | 合计 | |
男 | |||
女 | |||
合计 |
(3)将每周课外训练时间为4-6小时的称为“业余球迷”,已知调查样本中,有3名“业余球迷”是男生,若从“业余球迷”中任意选取2人,求至少有1名男生的概率.
附: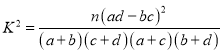 .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |