题目内容
17．利用行列式性质计算：$|\begin{array}{l}{3}&{2}&{6}\\{8}&{10}&{9}\\{6}&{-2}&{21}\end{array}|$．分析 利用三阶行列式对角线展开法则求解．
解答 解：$|\begin{array}{l}{3}&{2}&{6}\\{8}&{10}&{9}\\{6}&{-2}&{21}\end{array}|$
=3×10×21+8×（-2）×6+2×9×6-6×10×6-2×8×21-9×（-2）×3
=-420．
点评 本题考查三阶行列式的计算，是基础题，解题时要熟练掌握三阶行列式对角线展开法则．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
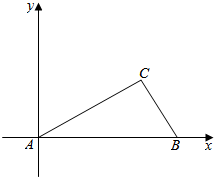如图，一边在x轴，一个顶点在原点△ABC的所有高都小于1，请问是否存在这样的B、C的位置，使得△ABC的面积大于2015？
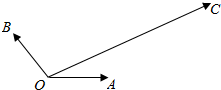如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°，|$\overrightarrow{OC}$|=2$\sqrt{3}$，用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$．
9．已知f（x）是定义在R上的偶函数且在[0，+∞）上递增，p：f（$\frac{x}{x+1}$）＜f（-$\frac{1}{2}$），q：|x-a|＜1，若p是q的充分不必要条件，则实数a的取值范围为（ ）
| A． | （0，$\frac{4}{3}$） | B． | （-∞，0）∪（$\frac{4}{3}$，+∞） | C． | （-∞，0]∪[$\frac{4}{3}$，+∞） | D． | [0，$\frac{2}{3}$] |