题目内容
8.已知函数,f(x)是定义在R上的奇函数,它的图象关于直线x=1对称,且f(x)=x(0<x≤1).若函数y=f(x)-$\frac{1}{x}$-a在区间[-10,10]上有10个零点(互不相同).则实数a的取值范围是$[-\frac{1}{10},\frac{1}{10}]$.分析 根据f(x)的图象关于x=1对称得f(1+x)=f(1-x),由f(x)是R上的奇函数求出函数的周期,再画出f(x)和y=$\frac{1}{x}$的图象(第一象限部分),由图得函数y=f(x)-$\frac{1}{x}$-a在区间[-10,10]上有10个零点的条件,列出不等式组求出实数a的取值范围.
解答 解:因为f(x)的图象关于x=1对称,所以f(1+x)=f(1-x)
因为f(x)是R上的奇函数,所以f(x+1)=-f(x-1).
所以f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x).
则f(x)是周期为4的函数,
由f(x)=x(0<x≤1)画出f(x)和y=$\frac{1}{x}$的图象(第一象限部分):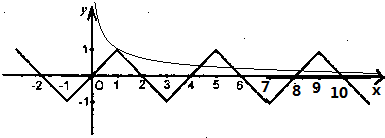 .
.
因为函数y=f(x)-$\frac{1}{x}$-a在区间[-10,10]上有10个零点,
所以y=f(x)与y=$\frac{1}{x}$+a在区间[-10,10]上有10个不同的交点,
因为y=f(x)与y=$\frac{1}{x}$是奇函数,所研究第一象限的部分交点问题即可,
而y=$\frac{1}{x}$+a的图象是由y=$\frac{1}{x}$的图象上下平移得到,
由图得,向上平移时保证图象第三象限的部分在x轴的下方,则第一象限的部分有4个交点,
第三象限的部分有6个交点,
同理向下平移时保证图象第一象限的部分在x轴的上方,则第一象限的部分有6个交点,
第三象限的部分有4个交点,即$\left\{\begin{array}{l}{-\frac{1}{10}+a≤0}\\{\frac{1}{10}+a≥0}\end{array}\right.$,解得$[-\frac{1}{10},\frac{1}{10}]$.
故答案为:$[-\frac{1}{10},\frac{1}{10}]$.
点评 本题考查函数的周期性、奇偶性、对称性的综合应用,图象平移问题,以及反比列函数的图象,考查数形结合,数形结合是高考中常用的方法,属于难题.

| A. | 椭圆 | B. | 线段 | C. | 圆 | D. | 直线 |
