Question

2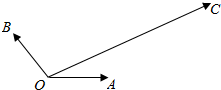．如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°，$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°，|$\overrightarrow{OC}$|=2$\sqrt{3}$，用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$．

Answer 1

分析 把$\overrightarrow{OC}$利用向量加法的平行四边形法则或三角形法则来表示成与$\overrightarrow{OA}$，$\overrightarrow{OB}$共线的其它向量的和向量，再由平面向量基本定理，即可得到．

解答 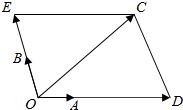解：如图，$\overrightarrow{OC}$=$\overrightarrow{OD}$+$\overrightarrow{OE}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$，
在△OCD中，∠COD=30°，∠OCD=∠COB=90°，
可求|$\overrightarrow{OD}$|=$\frac{|\overrightarrow{OC}|}{cos30°}$=4，
即有|$\overrightarrow{OE}$|=$\sqrt{16-12}$=2，
∴λ=4，μ=2，
则$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$．
故答案为：$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$．

点评 本题考查平面向量加法的平行四边形法则及解三角形，是一道综合题．